Ontology Intrinsic Completeness ________________________________________________________________________________________

Ph. A. Martin ^{[0000-0002-6793-8760]}   and, for the sections 3 and 5.2 to 5.4, O. Corby ^{[0000-0001-6610-0969]}

Comparison with a previous article. This article strongly extends some ideas of a previous article (focused on the notion of “comparability between objects”) by focusing on the more general notion of ontology completeness: the absolute or relative number of objects (in the evaluated KB) that comply to a specification (of particular relations that should exist between particular objects) given by a user if the evaluated KB. Indeed, the way it was defined in the previous article, comparability can retrospectively be seen was a specialization of completeness: this was convenient for the previous article but not generic enough for evaluating an ontology completeness. More precisely, in this previous article, comparability between objects is defined as i) checking that identity/equivalence relations or negations of them exist between these objects (this step is not mandatory with ontology completeness), and then ii) checking a particular completeness of objects wrt. a given set of particular (kinds of) relations (the present article introduces a model that supports the specification and checking of more subkinds of completeness).

Abstract for Section 2 (“Generic Specification Model”; this part is to be converted into an article; the sentences giving additional information that is not in this other article are in “olive” color; + in October 2022: comments or texts from OC are in this blue, my first texts/comments in answer to them is in this red (or green) and my my last texts/comments to them is in this orange.
In the field of ontology quality evaluation, a classic general definition of the completeness of an ontology – or, more generally, a knowledge base (KB) – is: the degree to which information required to satisfy a specification are present in this KB. A restriction of this general definition is often adopted in the domain of information systems ontologies: the ontological contents must be exhaustive with respect to the domain that the ontology aims to represent. Thus, most current completeness measures are metrics about relatively how many objects from a reference KB (an idealized one or another existing KB) are represented in the evaluated KB. In this article, they are called “extrinsic completeness” measures since they compare the evaluated KB to an idealized one or another existing KB, hence an external KB. Instead, this article focuses on “intrinsic (ontology/KB) completeness”: how many – or how relatively many – objects in the evaluated KB comply to a specification about particular relations that should exist from/to/between particular objects in this KB. Such specifications are typically KB design recommendations: ontology design patterns, KB design best practices, rules from methodologies, etc. These particular KB design recommendations do not refer to a reference KB. There are many KB checking tools or knowledge acquisition tools that implement the checking of some particular design recommendations. This article goes further: it proposes a generic model (an ontology of intrinsic completeness notions) and a tool exploiting it which i) enable their users to formally specify their own intrinsic completeness measures, and then ii) enable the automatic checking of the compliance of a KB to these measures. The first point thus also supports the formal definition and extension of existing KB design recommendations and the specification of KB quality measures not usually categorized as completeness measures. The genericity of the cited model and the automatic checkability of specifications based on this model are based on i) some specializations of a generic function with knowledge representations (KRs) or other functions as parameters, ii) the exploitation of the implication-related feature of any inference engine selected by the user for parsing and exploiting these above cited parameters, and iii) the idea that the KB must explicitly specify whether the relations from the specifications are true (or false) or in which context they are true (or false), e.g., when, where, according to whom, etc. To sum up, these last three points answer several research questions that can be merged into the following one: how to support KB users (or KB design recommendations authors) in defining intrinsic completeness measures that are automatically checkable whichever the used formalism and inference engine? One advantage is to extend the KB quality evaluations that someone can perform, Then, since the result can point to the detected missing relations, this result is also useful for knowledge acquisition purposes, e.g. for increasing the inferences that the KB supports or for representing relations to support the FAIR principles (Findability, Accessibility, Interoperability, and Reuse of digital assets). As illustrations of experimental implementations and validations of this approach, this article also shows i) an implemented interface displaying interesting types of relations and parameters to use for checking intrinsic completeness, and ii) some results of the evaluation of some well known foundational ontologies.

Keywords: Ontology completeness ⋅ KB quality evaluation ⋅ Ontology design patterns ⋅ Knowledge organization ⋅ OWL ⋅ SPARQL

Table of Contents

1. Introduction 2. General Approach: An Ontology-based Genericity Wrt. Goals, Formalisms and Inference Engines 2.1. The Function C*, its Kinds of Parameters and Specializations; Terminology and Conventions 2.2. Some Examples and Definitions of Existential Or Universal Completenesses 2.3. Genericity Wrt. Formalisms and Inference Engines 2.4. Some Advantages of Universal Completeness (and of Existential Completeness) 2.5. Comparison of the General Approach With Some Other Approaches or Works 2.6. Overview of Important Kinds of Parameter Values Via a Simple User Interface 2.7. Ontology of Operators, Common Criteria or Best Practices Related to Intrinsic Completeness 2.8. Evaluation of the General Approach Wrt. Subtype Or Exclusion Relations In Some Foundational Ontologies 3. Implementations Via a SPARQL Engine Exploiting an OWL Inference Engine 3.1. Exploiting OWL, SPARQL and SHACL For Checking Or Stating Relations Between Types 3.1.1. Using SPARQL Queries To Check Some OWL-RL/QL Relations Between Types 3.1.2. Types To State Or Check That Particular Types Are Related By Subtype Or Equivalence Relations, Or Cannot Be So 3.1.3. Checking Classes Via SHACL 4. Ontology and Implementations of Notions Useful For the 3^rd Parameter 4.1. Exploitation of All Relations Satisfying Particular Criteria 4.2. Object Selection Wrt. Quantifiers and Modalities 4.3. Minimal Differentia Between Particular Objects 4.4. Constraints on Each Shared Genus Between Particular Objects 4.5. Synthesis of Comparisons With Other Works 5. Ontology and Exploitation of Relation Types Useful For the 2^nd Parameter 5.1. Generic Relations For Generalizations Or Implications, and Their Negations, Hence For Inference Maximization 5.2. Interest of Checking Implication and Generalization Relations 5.2.1. Examples of Inconsistencies Detected Via SubtypeOf Relations and Negations For Them 5.2.2. Reducing Implicit Redundancies Between Types By Systematically Using SubtypeOf or Equivalence Relations (and Negations For Them) 5.2.3. Increasing Knowledge Querying Possibilities 5.2.4. Exploitation of Implication and Exclusion Relations Between Non-Type Objects 5.3. Exploitation of “Definition Element” Relations and Their Exclusions 5.3.1. Definition of "Definition Element" 5.3.2. Avoiding All Implicit Redundancies and Reaching Completeness Wrt. All “Defined Relations” 5.3.3. Finding and Avoiding Most Implicit Redundancies 5.4. Exploitation of Some Other Transitive Relations and Their Exclusions 5.5. Exploitation of Type Relations and Their Exclusions 5.6. Synthesis of Comparisons With Other Works 6. Conclusion 7. References

1. Introduction

KB quality. As detailed in [Zaveri et al., 2016], a survey on quality assessment for Linked Data, evaluating the quality of an ontology – or, more generally, a knowledge base (KB) and even more generally, a dataset  – often involves evaluating various dimensions such as i) those about the accessibility of the dataset (e.g. those typically called Availability, Licensing, Interlinking, Security, Performance), and ii) other dimensions such as those typically called Interoperability, Understandability, Semantic accuracy, Conciseness and Completeness.

Dataset completeness. As noted in [Zaveri et al., 2016], dataset completeness commonly refers to a degree to which the “information required to satisfy some given criteria or query” are present in the considered dataset. Seen as a set of information objects, a KB is a dataset (in [Zaveri et al., 2016] too). The KB objects, alias resources, are either types or non-type objects. These last ones are either statements or individuals. A statement is an asserted non-empty set of relations. In the terminology associated to the RDF(S) model [w3C, 2014a], relations are binary, often loosely referred to as “properties” and more precisely as “property instances”.

Extrinsic (dataset) completeness. A restriction of the previous general definition for ontology completeness is often adopted in the domain of information systems ontologies: “the ontological contents must be exhaustive with respect to the domain that the ontology aims to represent” [Tambassi, 2021]. In KB quality assessment surveys referring to the completeness of an ontology or KB, e.g. [Raad & Cruz, 2015] and [Zaveri et al., 2016] and [Wilson et al., 2022], this notion measures whether “the domain of interest is appropriately covered” and this measure involves a comparison to existing or idealized reference KBs or to expected results when using such “external” KBs – hence, this article calls this notion “extrinsic model based completeness”. E.g., completeness oracles [Galárraga & Razniewski, 2017], i.e. rules or queries estimating the information missing in the KB for answering a given query correctly, refer to an idealized KB. [Raad & Cruz, 2015] distinguishes “gold standard-based”, “corpus-based” and “task-based” approaches. [Zaveri et al., 2016] refers to schema/property/population completeness, and almost all metrics it gives for them are about relatively how many objects from a reference dataset are represented in the evaluated dataset.

Intrinsic (KB) completeness. This article gives a generic model allowing the specification of measures for the “intrinsic completeness” notion(s), not the extrinsic one(s). For now, these measures can be introduced as follows: each of them is a metric about how many objects – or relatively how many objects – in a given set comply to a semantic specification, i.e. one that specifies particular (kinds of) semantic relations that each evaluated object should be source or destination of. E.g., each class should have an informal definition and be connected to at least one other class by either a subclass/subclassof relation or an exclusion relation. As detailed in the next paragraph, such specifications can typically be KB design recommendations: ontology design patterns, KB design best practices, rules from methodologies, etc. These particular KB design recommendations do not refer to a reference KB or to the real world. Thus, this notion is not similar to the “ontology completeness” of [Grüuninger & Fox, 1995] where four “completeness theorems” define whether a KB is complete wrt. a specification stated in first-order logic. In [Zaveri et al., 2016] and [Wilson et al., 2022], the word “intrinsic” instead means “independent of the context of use” and the intrinsic completeness of this article is i) not referred to in [Zaveri et al., 2016], and ii) referred to via the words “coverage” (non-contextual domain-related completeness) or “ontology compliance” (non-contextual structure-related completeness) in [Wilson et al., 2022].

Purposes. Unlike extrinsic model based completeness, intrinsic completeness is adapted for evaluating the degree to which a given set of objects complies with KB design recommendations, such as particular ontology patterns [Presutti & Gangemi, 2008] [Dodds & Davis, 2012] (and the avoidance of anti-patterns [Ruy et al., 2017] [Roussey et al., 2007]), best practices [Mendes et al., 2012] [Farias et al., 2017] or methodologies (e.g. Methontology, Diligent, NeOn and Moddals [Cuenca et al., 2020]). Such an evaluation eases the difficult task of selecting or creating better KBs for knowledge sharing, retrieval, comparison or inference purposes.

Need for a generic specification model. Many KB evaluation measures can be viewed as intrinsic completeness measures for particular relation types. Many checks performed by ontology checking tools also evaluate particular cases of intrinsic completeness, e.g. OntoCheck [Schober et al., 2012], Oops! [Poveda-Villalón et al., 2014], Ontometrics [Reiz et al., 2020], Delta [Kehagias et al., 2021], and OntoSeer [Bhattacharyya & Mutharaju, 2022] (this last one and OntoCheck have been implemented as plug-ins for the ontology editor Protégé). However, it seems that no previous research has provided a generic way to specify intrinsic completeness measures (in an executable way) and thence enable their categorization and application-dependent generalizations (executable non-predefined ones), whichever the evaluated kinds of relations. It is then also difficult to realize that many existing KB evaluation criteria or methods are particular cases of a same generic one.

Related research questions. In addition to this genericity issue, some research questions – which are related and apparently original – are then: i) how to define the notion(s) of intrinsic completeness, more precisely than above, not only in a generic way but also one that is automatically checkable, ii) how to extend KB design recommendations and represent knowledge for supporting an automatic checking of the use of particular relations while still allowing knowledge providers to sometimes disagree with such a use (this for example rules out checking that a particular relation is asserted whenever its signature allows such an assertion), and iii) how to specify intrinsic completeness for the increase or maximization of the entering of particular relations by knowledge providers and then of inferences from these relations (e.g., especially useful relations such as subtype and exclusion relations, or type relations to useful meta-classes such as those of the OntoClean methodology [Guarino & Welty, 2009])? When the representations have to be precise or reusable – as is for example the case in foundational or top-level ontologies – these questions are important.

Use of generic functions; insufficiencies of constraints and axioms. To answer these research questions, this article introduces an ontology-based approach which is generic with respect to KRLs, inference engines and application domains or goals. The starting point of this approach is the use of C*, one possible polymorphic function theoretically usable for checking any of the intrinsic completenes notions described in this article. Any particular set of parameters of C* specifies one particular intrinsic completeness check. For practical uses, restrictions of C* are also defined, e.g. CN (which returns the number of specified kinds of objects in the specified KB) and C% (which returns the percentage of specified kinds of objects in the specified KB). Descriptions about C* are also about its restrictions. From now on, the word “specification” refers to an intrinsic completeness specification for a KB, typically via C% since it allows the checking of a 100% compliance. Checking a KB via a function like C% – or a query performing this particular check – is not like adding an axiom or a logic-based constraint to ensure that the KB complies to it. Indeed, axioms and classic kinds of constraints do not give percentages or other results and, since they generally have to be written within a KB, they are generally not usable for comparing KBs without copying or modifying them. Using functions (such as C% or within a constraint) also has advantages for clarity, concision and modularity purposes, as well as for lowering expressiveness requirements. One reason is that a function can encapsulate many instructions, sub-functions or rules, and can support default parameters. Second, a function allows the components of a specification to be distributed onto different parameters. Thus, the KRL or constraint-language required for writing the parameters does not have to be as expressive as the one that would be required for writing an axiom or a constraint instead of the function call. Furthermore, identifying these parameters and useful values for them is a first step for creating an ontology of (elements for) intrinsic completeness. As later illustrated, several useful kinds of such elements would require a second-order logic notation to be used in axioms or constraints, i.e., without the kinds of functions or special types described in this article. Most KRLs and constraint languages do not have such an expressiveness. As another example, except in particular cases, SHACL-core [w3c, 2017] cannot (but SHACL-SPARQL can) specify that particular objects of a KB (e.g. classes) should be connected to each other via particular relations (e.g. exclusion relations) is a negated or positive way (i.e. with or without a negation on these relations). Yet, this article shows that this kind of specification is very useful and often easy to comply with.

Section 2: the general approach.

• Section 2.1 starts the description of this above cited ontology – and introduces the approach – via a description of the parameters of C* and its restrictions. For genericity purposes, C* can exploit contextualizing meta-statements for taking into account such constraints as well as modalities and negations. This also allows the generalization of existing KB design recommendations to make them easier to comply with: relations following the advocated relations may also be negated or contextualized. This article does not advocate any particular KB design recommendations, it identifies interesting features for intrinsic completeness and a way to allow KB users to exploit these features and combine them.
• Section 2.2 provides examples and formal definitions for kinds of specifications which are simple but already generally more powerful than existing intrinsic completeness measures (which, in addition, unlike here, are hard-coded).
• Section 2.3 discusses the genericity of the approach with respect to KRLs and inference engines, while Section 2.5 compares this general approach with some other approaches or works. Presenting examples before these two sections help better understand these two sections and avoids making them over-general. Similarly, if the above research questions or statements of the problems still seem abstract, the examples instantiate these points and avoid the need for a separate section for them.
• Section 2.4 presents advantages of two very general kinds of intrinsic completeness introduced in Section 2.2: i) one here called “existential completeness” which underlies most other works related to intrinsic completeness measures, and ii) an original and more powerful one here called “universal completeness”. Although this article does not advocate any particular intrinsic completeness check, Section 2.4 shows that universal completeness not only maximizes the checking of the specified relation types but, from some viewpoints, is relevant to use (as a better KB quality measure) whenever existential completeness is.
• The proposed approach is supported by a Web-accessible tool at http://www.webkb.org/.../??? and, for this tool, Section 2.6 shows a simple user interface. This one gives an overview of the various kinds of parameters and useful kinds of values for these parameters. More values are proposed in Section 4 and Section 5.
• Section 2.7 proposes an ontology of operators, common criteria or best practices related to intrinsic completeness. This ontology is a way to complete the comparisons of Section 2.5 and the overview and inter-relations of Section 2.6.
• Section 2.8 evaluates the general approach with respect to subtype or exclusion relations in some foundational ontologies.

Section 3: implementation in SPARQL+OWL. This section shows how OWL and SPARQL [w3c, 2013a] (or SHACL [w3c, 2017]) can be used to i) implement CN–, CN and C% for evaluating intrinsic completeness via strict subtype relations, exclusion relations and equivalence relations, and ii) efficiently build such a KB. Section 4 and Section 5 reuse the framework for proposing SPARQL+OWL queries that implement more complex specifications.

Section 4: ontology and implementations of notions useful for the 3^rd parameter of C*. This section generalizes Section 2.6 for the specification of useful constraints on relations between particular objects in the KB (e.g., regarding “genus and differentia” structures), once the source objects and the types of relations from them have been specified.

Section 5: ontology and exploitation of relation types useful for the 2^nd parameter of C*. This section generalizes Section 2.6 regarding the specification of transitive relations – especially, generalization, equivalence and exclusion relations – as well as exclusion relations and instanceOf relations. This section also presents the advantages of using such specifications for maximizing inferences and, more specifically, for search purposes as well as the detection of inconsistencies and redundancies.

2. General Approach: an Ontology-based Genericity Wrt. Goals, Formalisms and Inference Engines

2.1. The Function C*, its Kinds of Parameters and Specializations; Terminology and Conventions

C* and the kinds of parameters it requires. Theoretically, a complex enough function – here named C* – could implement all elsewhere implemented intrinsic completeness checks, although its code might have to be often updated to handle new features. Since the basic kinds of data used by C* can be typed and aggregated in many different ways, C* could be defined in very different ways, using different kinds of parameters, i.e. different signatures, even when using “named parameters” (alias “keyword arguments”, as opposed to positional parameters). For C* to be generic (including wrt. KRLs), C* must allow the use of only one parameter – one logic formula or boolean test function – fully describing which particular objects must have which particular relations to which particular objects (or, equivalently, which particular relations must exist between which particular objects). As examples in later subsections illustrate, for readability and ease of use purposes, this description of objects and relations that must exist should also decomposable into more than one parameter, and two parameters that are themselves sets seem sufficient. In any case, C* has to be polymorphic: for each parameter, C* should accept different kinds of objects. E.g., for an object selection parameter, C* should at least accept i) a pre-determined set of objects, ii) a set of criteria to retrieve such objects in the specified KB, and iii) a function or a query to make that retrieval. In this article, to ease the readability and understanding of the proposed handy restrictions of C*, positional parameters are used and the selected untyped signature of C* is “(objSelection1, objSelection2, constraints, metric, nonCoreParameters)”. The following points describe this list of parameters and their rationale. For the reasons given in the introduction, since this list is also an informal top-level ontology for some elements for intrinsic completeness, a constraint language may also address the described notions and supports their representation within the range of its expressiveness. E.g., in SHACL, objSelection1, objSelection2 and constraints are respectively addressed via the relations sh:target, sh:property (along with sh:path) and sh:constraints.

• Together, objSelection1 and objSelection2 specify the set of objects and/or relations to be checked, i.e. i) the set of objects from which particular relations are to be checked, and/or ii) the set of particular relations to check, and possibly iii) the set of objects that the destinations of the checked relations may be. In the following examples below using the two parameters.
  • objSelection1 specifies the set of objects to be checked in the evaluated KB. E.g., the expression PL_`∀x rdfs:Class(x)' can be used to specify in a classic Predicate Logic notation that this set is composed of every class in the KB. For readability purposes, this article also proposes and uses FS (“For Sets”), a set-builder (or list comprehension) notation. FS_{every owl:Thing} is equivalent to the previous PL expression, while FS_{every owl:Thing} specifies a set composed of all the (named or anonymous) objects (types, individuals or statements) represented in the KB (it is therefore advisable to use expressions that are more constrained than this one).
  • objSelection2 specifies the types of relations from the objects referred to by objSelection1. E.g. the expression “FS_{rdfs:subClassOf, owl:equivalentClass}” means that subClassOf relations and equivalentClass relations from those objects should be checked.
  • The set of possible destination objects for these relations is not specified: by default, any destination is allowed.
• The 3^rd parameter specifies constraints that the “objects and/or relations selected via the first two parameters” should comply with. Example of constraint: for each selected object and selected relation type, there should be at least one relation of that type from this object.
• The 4^th parameter specifies the metric to be used for reporting how many – or relatively how many – of the “objects and/or relations selected via the first two parameters” comply with the “constraints specified via the 3^rd parameter”. Examples of metrics and metric names are: i) “N_obj”, the number of compliant selected source objects, ii) “N_rel”, the number of compliant relations from or to the selected objects, iii) “L_obj–”, the list of non compliant source objects, iv) “%_obj”, the ratio of N_obj to the number of selected objects, v) “%_rel”, the ratio of N_rel to the number of selected relations, and vi) “%%_obj”, the average of the percentage of compliant relations from or to each of the selected objects. More complex metrics can be used, such as those of the kinds described in [Hartmann et al., 2005] (e.g. “precision and recall” based ones) and [Ning & Shihan, 2006] (e.g. “Tree Balance” and “Concept Connectivity”) or those used in Ontometrics and Delta.
• The 5^th parameter specifies objects that are not essential to the specification of an intrinsic completeness, e.g. parameters about how to store or display results and error messages. Hence, this parameter is not mentioned anymore in this article.

To sum up, the above distinctions (<selections, constraints, metric>) and associated parameters seem to support the dispatching of the basic kinds of data required by C* into a complete set of exclusive categories for these basic kinds of data, i.e., into a partition for them. Thus, all the data can be dispatched without ambiguities about where to dispatch them. The above parameters can also be seen as a handy way to describe part of the model used in this article (a more common way to describe a model is to define tuples of objects).

CN, CN–, C% and C%% as handy restrictions of C*. CN, CN–, C% and C%% only have the first three parameters of C*.  Using CN is like using C* with the N_obj metric as 4^th parameter. Section 2.2 formally defines CN for some combinations of parameters. That formal definition can be adapted for other combinations of parameters. CN– is like C* with the L_obj– metric (this one is more useful during KB building than when comparing KBs).  C% is C* with the %_obj metric, while C%% is C* with the %%_obj metric. This article provides many examples of calls to C% and CN, and thus of how C* functions can be used. C%% is also used in Section 2.8 for analyzing and comparing some top-level ontologies.

Taking into account (or not) negations and, more generally, contexts. In this article, i) a statement is a relation or a non-empty set of relations, and ii) a meta-statement is a statement that is – or can be translated into – a relation stating things about a(n inner) statement. A negated statement can be seen as – or represented via, or converted into – a statement using a “not” relation expressing a “not” operator. A meta-statement that modifies the truth status of a statement – e.g., via a relation expressing a negation, a modality, a fuzzy logic coefficient or that the inner statement is true only at a particular time or place or according to a particular person – is in this article called a contextualizing statement (alias, context) for its inner statement, the contextualized statement. Thus, a relation that changes the truth status of a statement is a contextualizing relation (e.g., a “not” relation, a modality relation to a “necessarily not” value, a probability coefficient of 0%; this article defines negation as a particular contextualization for simplifying several of its formal or informal expressions). A statement is either positive (i.e. without a meta-statement, or with a meta-statement that simply annotates it instead of contextualizing it), negative (alias, negated), or contextualized but not negated. With C* as above described, if more than one parameter is used, it is the third one that specifies the kinds of contexts that the checked relations may have or should have. Some examples in the next subsection illustrate formalizations of this taking into account of contexts, and its advantages, especially for generalizing KB design recommendations.

Rationale of the used terminology. In some KR related terminologies, unlike in this article, the word “relation” is only used for referring to a relationship between real-world entities while other words are used for referring to the representations of such relations, e.g. “predicate” in Predicate logics, “property” in RDF and some knowledge graph formalisms [Kejriwal, Knoblock & Szekely, 2021], or “edge” in another [Hogan et al, 2021]. In this article, the words “relation”, “types”, “statements”, “meta-statements” and “contexts” have the meanings given in the introduction because i) these are common meanings in KRLs in KRLs, e.g. in Conceptual Graphs [Sowa, 2000], and ii) these words are more intuitive, general (hence not tied to a particular formalism) and easy-to-use (e.g., the words "from" and "to" often have to be used in this article and associating them to the word “property” seems awkward). Thus, (KR) “objects” are either types, individuals and statements, and a type is either a class or a relation type.

Conventions and helper ontologies. Identifiers for relation types have a lowercase initial while other object identifiers have an uppercase initial. “OWL” refers to OWL-2 [w3c, 2012a]. “RDFS” refers to RDFS 1.1 [w3c, 2014a]. OWL types are prefixed by “owl:”, and RDFS types by “rdfs:”. The other types used in this article are declared or defined in the following two ontologies.

• One of them is named “Sub” [Martin, 2019] (a good part of it is about subtypes, subparts and similar relations; this ontology has over 200 types). This does not mean that Sub needs to be read for understanding this article; it just means that all the types used in this article are defined and organized within existing ontologies. E.g., Sub includes sub:owl2_implication, the most general type of implication that an OWL-2 inference engine can exploit or implement. The “sub:” prefix abbreviates the URL of Sub. In accordance with Section 2.3 (“Genericity Wrt. Formalisms and Inference Engines”), “=>” and symbols derived from it are not prefixed in the examples and definitions below. Two statements or two non-empty types are in exclusion if they cannot have a shared specialization or instance, i.e., if having one is considered an error. E.g., owl:disjointWith is a type of exclusion relation between two classes.
• The other ontology is named “IC” (for Intrinsic Completeness) [Martin, 2022 ??]. E.g., IC includes “intrinsic completeness checking cardinality types” such as ic:Every-object_to_some-object and ic:Every-object_to_every-object which are explained in the next subsection. IC also includes the declaration of the type for C* and its subtypes used in this article, e.g. ic:C% and ic:CN. In this article, for clarity purposes, these function types are not prefixed by “ic:”. Like Sub, IC does not need to be read for understanding this article.

2.2. Examples and Definitions of Existential Or Universal Completenesses

A very simple example: specifying that every class in a KB should have a label, a comment and a superclass. Since every class can have a superclass (for example since rdfs:Class is a subclass of itself), performing such a check can be a legitimate KB design recommendation. Whether it is a best practice is not relevant here: this article does not advocate any particular intrinsic completeness check, it identifies interesting features for intrinsic completeness and a way to allow KB users to exploit these features and combine them. Given the above cited conventions and descriptions of C*, here are some ways to specify this check using C% and various KRLs.

• With Predicate Logic (extended with the possibility to use “∈Kb” for referring to the objects – types, individuals or statements – represented in a KB identified as Kb): C%( PL_` ∀c∈Kb ∃label∈Kb ∃comment∈Kb ∃superclass∈Kb rdfs:label(c,label) ∧ rdfs:comment(c,comment) ∧ rdfs:subClassOf(c,superclass) ’ ). This function call gives the percentage of classes having the specified relations. This is also a specification: the ideal result should be 100%. If an object use relations specializing the mandated relations – e.g., by using subtypes of the mandated relation types – this object is still counted as complying with the specification. A statement that is in a parameter is not asserted in the KB: like a constraint, the inference engine cannot use it for deducing other formulas and adding them to the KB. However, this statement is written with a KRL, not a constraint language.
• Even for this very simple example, using Predicate logic (PL) may seem a bit cumbersome. With some other languages, e.g. RDF+OWL/Turtle, i.e. the RDF+OWL model with a Turtle notation, the specification would be more cumbersome but C* and derived functions ideally should or could use such languages too when they are expressive enough for representing the wanted specification. E.g., with RDF+OWL/Turtle, the previous specification could be:

  C%( RDF+OWL/Turtle_` [a owl:Class; rdfs:subClassOf [ owl:intersectionOf 
                         ( [a owl:Restriction;  owl:onProperty rdfs:label;  owl:minCardinality 1]
                           [a owl:Restriction;  owl:onProperty rdfs:comment;  owl:minCardinality 1]
                           [a owl:Restriction;  owl:onProperty rdfs:subClassOf;  owl:minCardinality 1]
                         ) ] ] ’ ).

  As with PL above, RDF+OWL/Turtle is here used for expressing a constraint but not a regular stand-alone one. Here the corresponding stand-alone constraint in SHACL-core:

    sub:Shape_for_a_class_to_have_a_least_a_label_and_a_comment_and_a_subclass
       a sh:NodeShape ;   sh:targetClass owl:Class ;
       sh:property [ sh:path rdfs:label ;  sh:minCount 1 ; ]
       sh:property [ sh:path rdfs:comment ;  sh:minCount 1 ; ]
       sh:property [ sh:path rdfs:subClassOf;  sh:minCount 1 ; ] .

• To cope with the increasing complexity of examples below, this article proposes the use of several parameters and, within them, i) FS, a Set-builder notation, and ii)  types with a definition that C* is supposed to interpret or that is hard-coded in C*. /*pm: this replaces "predefined constants" */ With them and in accordance with the descriptions of parameters given in Section 2.1, the previous specification can also be written as: C%( FS_{every rdfs:Class}, FS_{rdfs:label, rdfs:comment, rdfs:subClassOf}, FS_{ic:Every-object_to_some-object} ). The type ic:Every-object_to_some-object indicates that every object specified via the 1^st parameter should have some (i.e., at least one) relation of type rdfs:label and a (some) relation of type rdfs:comment and a relation of type rdfs:subClassOf. For an exact translation of the above Predicate Logic version, the type ic:Only_positive-relations_may_be_checked should also be specified to indicate that negated or contextualized relations of the three above cited relation types are not taken into account, i.e., checked. However, dropping this restriction is actually an advantage since it allows the taking into account of such relations even if they are contextualized. E.g., a label relation may be contextualized to state that a particular person gave a particular label to a particular class for a particular time (such representations may be easier to handle than searching and managing various versions of a KB). Similarly, in the case that some subtype relations are used for the categorization of animal species, some categorizations may be associated to some authors and time periods.

In this article, all sets are expressed in FS and hence, from now on, “FS_” is omitted. By default, these sets are AND-sets in the sense that all their elements are mandatory. However, via the prefix “OR”, OR-sets can be specified. E.g., using OR{rdfs:label, rdfs:comment, rdfs:subClassOf} as 2^nd parameter in the previous specification would mean that each class in Kb should have at least one relation of type rdfs:label or rdfs:comment or rdfs:subClassOf. The rest of this subsection use examples to show how a C* function call that uses FS can be translated into a C* function call that uses PL.

Definition of CN for basic existential completeness, with FS parameters and default values. Here, “basic” means without taking contexts into account. In this article, a completeness specification that uses ic:Every-object_to_some-object – or that can be translated into a specification using such a type – is referred to as specification of “existential completeness (wrt. relations of particular types)” – as opposed to the more useful “universal completeness” detailed below. With Kb being a KB or portion of KB, for any type OT and any set of binary relation types that is identified as RTs, calling  CN({every OT}, RTs, {ic:Every-object_to_some-object, ic:Only_positive-relations_may_be_checked}) returns the number of objects O1 satisfying the next formula.
Formula 1:  ∀O1∈Kb,rt∈RTs ∃O2∈Kb   OT(O1) ∧ (Kb => rt(O1,O2)).
For the above specification but with ic:Every-object_to_some-object replaced by ic:Every-object_to_some-other-object, it is sufficient to add “∧ (O1!=O2)” at the end of Formula 1.

Definition of CN for existential completeness, with FS parameters, default values, and taking contexts into account. With the same assumptions as for the previous definition but without the restriction ic:Only_positive-relations_may_be_checked – and, instead, with the restriction ic:The_checked-relations_may_be_negated-or-otherwise-contextualized – the function call returns the number of objects O1 satisfying the next formula (which looks like a tautology but, with the assumptions listed below, is not).
Formula 2:  ∀O1∈Kb,rt∈RTs ∃O2∈Kb   OT(O1) ∧ ( (Kb => rt(O1,O2)) ∨ (Kb => ¬ rt(O1,O2)) ∨
                       (Kb => (∃c sub:Contextualization(c) ∧ sub:contextualization( rt(O1,O2), c ) ) ) )
This formula – and, more generally, this article – makes the following assumptions.

• The “=>” symbol refers to the implication exploited by “the used inference engine”: the one with which the function makes inferences for comparing KB objects with specifications (this engine may be for example be implemented within the function or be an external engine called by the function). Section 2.3 justifies this choice and its interest for the independence ot the approach with respect to particular logics and inference engines. The operator “¬” (alias, “!”) is the classic negation operator. The above formula is only a description of each check that the function must here perform: “(Kb => rt(O1,O2)) ∨ (Kb => ¬ rt(O1,O2))” is not supposed to be interpreted as a tautology but to mean that there should be a check that a positive or negated rt relation (inferred or explicitly entered) exists between O1 and O2. Thus, if an external inference engine is used and if this one would simplify the above expression into a tautology before checking each of the two implications, this engine must for example be called twice: once for checking the first implication and another time for checking the second implication.
• This formula assumes that each statement (in the KB) that implicitly or explicitly uses contextualizations has been translated – or can be translated by the inference engine – into a statement that uses sub:contextualization (the relation type for all binary relations from a statement to a contextualizing condition or value) and hence, indirectly, sub:Contextualization, the type for all contextualizing conditions or values. Thus, the “(Kb => ¬ rt(O1,O2))” part of Formula 2 is actually redundant; it is kept here for explanation purposes.

This formula – and the other ones given in this article – can easily be adapted for non-binary relations.

Definition of C% wrt. CN. C% divides the result of CN by the number of evaluated objects. With the previous example, since the 1st parameter specifies the set of evaluated objects, using C% instead of CN means dividing this result of CN by the number of objects of type OT.

Definition of CN– wrt. the PL formula for CN. CN– returns the list of objects for which the PL formula for CN (i.e. Formula 1 in the previous example).

Simple example of universal completeness: specifying that every class in a KB should be explicitly represented as exclusive or non-exclusive with every other class in the KB. Some advantages of such a specification or of derived ones are summarized in Section 2.4, along with reasons why, at least from some viewpoints, such specifications are always possible to comply with. In this example, the goal is to specify that every pair of classes should be connected by an inferable or directly asserted, negated or not, relation of type owl:disjointWith. The negation of an owl:disjointWith relation can be represented in various ways. (To help RDF+OWL users represent that two classes are not disjoint, Sub uses RDF+OWL/Turtle to fully define the relation type sub:non-equivalent_nor_exclusive_class as well as other more handy-to-use relation types or collection types.) Analogously to the previous examples, here are some ways to represent this specification using C%:

• With PL (with the previously cited extension):  C%( PL_`∀c1,c2∈Kb  (Kb => owl:disjointWith(c1,c2)) ∨ (Kb => ¬ owl:disjointWith(c1,c2))’ ), assuming that the used inference engine (the one that checks this specification; this notion is detailed in Section 2.3) does not use the closed-world assumption and does not handle the formula as equivalent to the following tautology in traditional logics:  ∀c1,c2∈Kb  Kb => (owl:disjointWith(c1,c2) ∨ ¬ owl:disjointWith(c1,c2)) .
• Even in this simple example, universal completeness cannot be expressed with RDF+OWL/Turtle. Using owl:allValuesFrom and owl:NegativePropertyAssertion would not lead to a solution. However, as shown in Section 3, a SPARQL endpoint with an OWL profile [???] (hence also being or exploiting an OWL inference engine) can be used checking such a specification.
• With FS:  C%( {every rdfs:Class}, {owl:disjointWith}, {ic:Every-object_to_every-object, ic:The_checked-relations_may_be_negated} ). However, for the specification to be more intuitively understood when reading it, some persons would like the ic:The_checked-relations_may_be_negated indication to be within the 2^nd parameter, right by the types of the checked relations. For these persons, the C* functions allow the use of a particular structure (in the 2nd parameter) which makes the next specification equivalent to the previous one: C%( {every rdfs:Class}, { ic:The_checked-relations_may_be_negated {owl:disjointWith} }, {ic:Every-object_to_every-object} ). As this example illustrates, this particular structure is a set containing a set of relation types and a set of constraint types about the use of these relation types: since this structure can easily be recognized by a C* function and is unlikely to be useful for another purpose in a 2^nd parameter, this structure can be dedicated to allowing people indicate such constraint types in the 2^nd parameter instead of the 3^rd parameter. With this simple and KRL independent solution, unlike with the use of predefined keywords or the use of more complex expressions, most KRLs can still be used for writing this 2^nd parameter. To make the last specification even more intuitive to read, the type ic:With-or-without_negations (which IC defines as equivalent to ic:The_checked-relations_may_be_negated) can also be used: C%( {every rdfs:Class}, { ic:With-or-without_negations {owl:disjointWith} }, {ic:Every-object_to_every-object} ).

Definition of CN for universal completeness, with FS parameters. With the same assumptions as for Formula 2, calling  CN( {every OT}, RTs, {ic:Every-object_to_every-object, ic:The_checked-relations_may_be_negated-or-otherwise-contextualized} ) returns the number of objects O1 satisfying the next formula.
Formula 3:  ∀O1∈Kb,rt∈RTs,O2∈Kb   OT(O1) ∧ ( (Kb => rt(O1,O2)) ∨ (Kb => ¬ rt(O1,O2)) ∨
                       (Kb => (∃c sub:Contextualization(c) ∧ sub:contextualization( rt(O1,O2), c ) ) ) )
Since there may be many anonymous objects represented in a KB – in addition to named objects, i.e. those associated to an identifier – it is often better to use ic:Every-object_to_every-named-object (or a representation of what this type means) instead of ic:Every-object_to_every-object. With this added restriction, assuming the possibility to use “∈NamedObjects” for referring to the named objects of the evaluated KB, the formula for the previous specification is:
Formula 4:  ∀O1∈Kb,rt∈RTs,O2∈NamedObjects   OT(O1) ∧ ( (Kb => rt(O1,O2)) ∨ (Kb => ¬ rt(O1,O2)) ∨
                       (Kb => (∃c sub:Contextualization(c) ∧ sub:contextualization( rt(O1,O2), c ) ) ) )
Some languages provide a relation or a function to check whether an object is named. E.g., although RDF+OWL offers neither, SPARQL provides the isIRI function for such a check. From now on, the type ic:The_checked-relations_may_be_negated-or-otherwise-contextualized is assumed to be a default value in the 3^rd parameter and hence is generally left implicit.

Specification of exactly which contextualizing relation types should be taken into account. The IC ontology provides types (with hopefully intuitive names) for expressing particular constraint parameters for C*. Instead of such types, logical formulas should also be accepted by the C* functions for their users to be able to specify variants of such constraints when they wish to. Regarding contexts, this means that the users should be able to specify the contextualizing relation types that should be taken into account. To that end, IC provides the relation type ic:contextualizing-relation-type_taken-into-account. Here are examples of its use:

• In the 3^rd parameter of a C* function*, the constraint  FS_`every sub:Statement –––ic:contextualizing-relation-type_taken-into-account–––> {sub:negation, sub:time}’ states that every statement (hence, every relation) checked by the function is further checked only if it is positive, negated or contextualized in time via a sub:time relation. Indeed, in FS, for concision purposes, a set that is a destination of a relation is (by default) to be interpreted “distributively”, not “cumulatively”, i.e., each of the set members is a destination of the relation, not the set itself (the terminology of [Sowa, 2000] is here reused).
• If sub:time is omitted in this previous example (i.e., if only sub:negation remains in the set), the constraint becomes equivalent to the definition of ic:The_checked-relations_may_be_positive-or-negated-but-not-otherwise-contextualized. If sub:negation is omitted too (i.e., if the set is empty), the constraint now states that, for the specified check, there are no contextualizing relation types to be taken into account for the specified check. With respect to Formula 1, 2 and 3, these last two particular cases simply means removing the parts about negations and/or contexts (thus, for example, going from Formula 2 to Formula 1). However, from a specification viewpoint, i.e. with respect to the above cited set, indicating the type ic:Only_positive-relations_may_be_checked means indicating that this set is empty. Assuming that this set is named setOfConstraints, in PL this specification would be: PL_` ¬(∃constraint sub:member(setOfConstraints,constraint) ) ’. Still in PL, the general rule to exploit the content of this setOfConstraints would be:

   PL_` ∀stmt,constraint  ( sub:Statement(stmt) ∧ sub:member(setOfConstraints,constraint)
                          ) => sub:contextualizing-relation-type_taken-into-account(stmt,constraint) ’.

Mandatory contextualizing relations can be similarly specified.

Specification of the types of mandatory contextualizing relations. By using sub:contextualizing-relation-type_that_is_mandatory instead of sub:contextualizing-relation-type_taken-into-account, one may specify the types of the contextualizing relations that are mandatory for the checked relations, instead of just taken into account in the ways previously described. With respect to the formulas 2 to 4, and with MRTs referring to a set of mandatory binary relation types, this means replacing the “or” expression in these formulas by “(Kb => (∀mrt∈MRTs (∃c sub:Contextualization(c) ∧ mrt( rt(O1,O2), c ) ) ) )”. For instance, [any sub:Statement –––sub:mandatory-contextualizing-relation-types–––> {sub:time}] means that each of the relations specified to be checked should have a temporal contextualization. When the mandatory contextualizations exist but are not directly represented via a meta-statement – i.e., when they are implicit or represented in another way – these contextualizations should be inferred for the specified checking to work as expected. E.g., the KB may have hard-coded or explicitly represented rules stating that certain kinds of statements (typically, definitions) are true at any time.

Completeness of the destinations of each relation of particular types (possibly in addition to the existential or universal completeness wrt. relations of these types). Here are two examples for subclass relations.

• A call to C%( {every rdfs:Class}, {sub:subClass}, {[* → 1..* complete{...}]} ) returns 100% if every class that has at least one subclass has at least one set of subclasses that is complete (in the usual sense for such a set: each instance of the class is an instance of at least one of the subclasses; owl:unionOf relations can be used for representing such a set). The 3^rd parameter may also include other values, e.g., as in Section 2.2, the type ic:Every-object_to_every-named-object to specify that, from every class, the universal completeness wrt. subclass relations should also be checked.
• Similarly, C%( {every rdfs:Class}, {sub:subClass}, {[* → 1..* partition{...}]} ) returns 100% if every class that has at least one subclass has at least one “subclass partition”, i.e. a set of disjoint subclasses that is complete (in the same sense as in the previous point; owl:disjointUnionOf relations can be used for representing such a set).

Section 5.2 shows how such specifications can be used with partOf relations instead of subclassOf relations. More precisely, Section 5.2 includes definitions and an example showing how [* → 1..* complete{...}] can be used to ensure that every class has a definition stating that each of its individuals has a complete set of parts, in the sense that there cannot exist a part of the individual that is not identical or part of a member of this set of parts. The user interface introduced in Section 2.6 (Figure 1) includes these “completeness of the destinations” options in its menu for the 3^rd parameter.

2.3. Genericity Wrt. Inference Engines

Independence from particular logics and inference engines. For genericity purposes, the approach presented in this article is purposefully not related to a particular logic, KRL, inference engine or strategy. To that end, the explanations in this article refer to relations that are directly asserted or are “inferable” by “the used inference engine”, and the Predicate Logics formulas used for function definition purposes use the “=>” symbol which refers to the implication operator of the KRL exploited by the used inference engine. Although these above cited formulas are second-order logic formulas (since they quantify over relation types), they can be automatically downgraded – e.g., instantiated wrt. each of the types in the KB, similarly to Henkin's interpretation – to match the expressiveness of the KB objects that are checked, or equivalently, the required expressiveness of the (KRL exploited by) the used inference engine (the next paragraph expands on this point). Then, the logical properties of the checking function and approach are derived from those of the used “=>” and engine:

• If the used logic is “syntactically or semantically valid” (informally, both cases imply that if the premises of an implication is true, its conclusion cannot be false), then the approach is “syntactically or semantically valid”.
• If the formal system composed of the KB and the used logic is “semantically complete” (i.e., if all the tautologies of this system are provable), then C* gives all the results it should. If that system is not semantically complete, some compliant or non-compliant objects may not be retrieved.
• The computational properties of the function depends on i) which operation of the inference engine it calls – and how repetitively it is called – to perform the above cited search and matching, and ii) the computational properties of this operation: they depend on the entailment regime [w3c, 2013b] of the engine as well as the normalization [Vrandečić & Sure, 2007] and complexity associated to the exploited KRs (in OWL, this relates to the notion of “profile” [w3c, 2012b], e.g., OWL-2 EL is a fragment of OWL-2 [w3c, 2012a] that has “polynomial time reasoning complexity”; [w3c, 2012b] gives computational properties for each OWL-2 profile).

To conclude, although the results of the function depend on the selected inference engine, it can be said that the approach itself is independent of a particular inference engine. This kind of genericity is an advantage and, at least in this article, there would be no point in restricting the approach to a particular logic.

The approach has no predefined required expressiveness: the expressiveness required to check some KRs is at most the expressiveness of these KRs. In the previous subsection, the formulas 1, 2 and 3 use a slight extension to classic Predicate Logics and are also second-order formulas. However, these formulas are for definitions and explanations purposes. They do not imply that the proposed approach requires contexts or a second-order logic. There are several reasons for this.

• As above noted, second-order logic formulas can be automatically downgraded into first-order logic via methods like via Henkin's interpretation, and then can often be further downgraded via similar methods.
• When contexts are not used in a KB, there is no need to check for them, and hence the part related to contexts in formulas such as Formula 2 or Formulas 3 can omitted. In many KBs contexts are not needed or not used, or partial (or ad hoc) representations of them are used, e.g. i) exclusion relations can replace some uses of the “necessarily not” operator of athletic modal logic (or some uses of the “not” operator), and ii) contexts in general may for example be expressed via the “Context Slices” design pattern [Welty, 2010] or via statement reification (e.g., as in RDF) plus types for particular kinds of contexts. If the checking function does not understand the special meaning of ad hoc representations of contexts, its results may be incomplete or incorrect.
• For retrieving and checking objects or relations, intrinsic completeness checking functions may call – and thus reuse – a logic-based inference engine, but they may also use simple graph matching techniques (e.g., for performance purpose) if the completeness of their results is not fundamental or if the KB does not have KRs that could make the results incomplete. This last case is true for the ontologies evaluated in Section 2.1.5, given the graph matching techniques of WebKB-2 [Martin, 2011], the tool used for these evaluations. Like inference engines, graph matching techniques can be adapted to take into account partial (or ad hoc) representations of contexts.
• For many useful kinds of specifications, intrinsic completeness checking functions may also be implemented using a query language. The sections 3 to 5 of this article propose SPARQL+OWL queries as implementations of these functions for particular kinds of parameters (e.g., those of all the examples below related to the checking of classes), and these queries have been validated via Corese [Corby & Faron-Zucker, 2015], a SPARQL and OWL inference engine. The interface shown in Section 2.6 (Figure 1) is able to use both Corese and WebKB-2.

2.4. Some Advantages of Universal Completeness (and of Existential Completeness)

Universal completeness wrt. generalization, equivalence and exclusion relations between classes. The example specification of this subsection is C%( {every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass, owl:disjointWith}, {ic:Every-object_to_every-named-object, ic:The_checked-relations_may_be_negated-or-otherwise-contextualized} ). With the special structure introduced in the universal specification example of Section 2.2, and a shorter name for the last constraint type, an equivalent specification is: C%( {every rdfs:Class}, {ic:With-or-without_negations-or-contexts {rdfs:subClassOf, owl:equivalentClass, owl:disjointWith} }, {ic:Every-object_to_every-named-object} ). These calls returns 100% if every class in the KB is connected by a(n inferable or directly asserted) positive, negated or contextualized relation to every named class in the KB, for each of the three specified relation types. For instance, if a pair of classes is related by an rdfs:subClassOf relation, as well as a negated owl:equivalentClass relation (e.g., via the use of sub:non-equivalent_class which is defined in Sub as disjoint with owl:equivalentClass), an OWL inference engine can deduce i) these two classes are also related by a negated owl:disjointWith, i.e., they are not disjoint, ii) the subtype relation relating these two classes is actually strict, i.e., that the two classes are not equivalent, and iii) regarding relations between these two classes, for each of the three specified relation types, the KB complies with the specification.

The counterpart of this specification with existential completeness instead of with universal completeness, i.e. with ic:Every-object_to_every-named-object replaced by ic:Every-object_to_some-named-object, returns 100% if every class in the KB is source of a positive, negated or contextualized relation to some class in the KB, for each of the three specified relation types. The next three paragraphs respectively show that i) building a KB complying with a universal completeness specification such as the previous one does not necessarily require entering much more lines than when not complying with it, ii) at least from some viewpoints, building such a KB is always possible and this KB is of better quality than if it only complies with its existential completeness counterpart, and iii) this particular universal completeness specification has at least three interesting particular advantages. The last two of these three paragraphs exploit the fact that in a KB complying with a universal specification, the number of relations with the specified relation types is, in a sense, maximal: in a KB complying with the previous universal completeness specification, the number of (positive or negated) (inferable or directly asserted) relations of the three above cited types between named classes cannot be augmented, hence the number of inferences that can be drawn based on these relations is also maximal in that same sense.

Building a KB complying with a universal completeness specification does not necessarily involve much extra work. At least for the previous example specification, building a KB complying with it does not require entering much more lines than when not complying with it if the following two conditions are met (as can most often be the case).

• The used inference engine is able to deduce many of the required relations, e.g., based on the used top-level ontology. For instance, the engine needs to be able to deduce that the subtypes of a type are disjoint with its disjoint types and then also cannot subtype – nor be equivalent to – these disjoint types.
• Knowledge providers use (directly or via some syntactic sugar) short ways of expressing combinations of relations of the above cited kinds, e.g. via collections such as owl:disjointUnionOf collections or else owl:unionOf collections. To provide these short ways, the Sub ontology defines many relation types, e.g. sub:sC which is a strict subclassOf relation type such that the subclass is neither exclusive to, subtype nor supertype of any of its siblings. OWL is sufficient for fully defining sub:sC within Sub (but this is not the case for its profiles OWL-EL, OWL-QL and OWL-RL [w3c, 2012b]).

Possibility and relevancy of complying with a universal completeness specification when complying with its existential completeness counterpart is relevant. Here, different uses of ontologies – and then viewpoints on them – must be distinguished:

• Most existing definitions for the word “ontology” focus on its goal – e.g., as an “explicit specification of a conceptualization” and “domain conceptualization” [Gruber, 2016] – or on the idea that this conceptualization “takes the form of the definitions of representational vocabulary (classes, relations, and so forth), which provide meanings for the vocabulary and formal constraints on its coherent use” [Gruber, 2016]. When general knowledge sharing (GKS) or reuse is the goal, this common viewpoint is from now on here named the “formal GKS viewpoint”. With this viewpoint, the more constrained the definitions, the more inferences can be made based on them (e.g., for checking that some objects or relations are correctly used and not misinterpreted) and hence the better the quality of the KB. This often increases the (re-)usability of the KB and never decreases it: providing precise types does not prevent also providing more general versions of them nor prevent users to add these generalizations. Adding constraints also means adding relations between objects. When the designer of an application finds that some of these relations are not useful for this particular application, this designer can filter them out, i.e., eliminate them from the KB of this application (this removal is likely to decrease the reusability of this last KB for other applications, but this may not be important for the designer of a particular application). A first conclusion is that, from this formal GKS viewpoint, a universal completeness specification can always be complied if it uses – or is equivalent to a specification using – the type ic:The_checked-relations_may_be_negated-or-otherwise-contextualized, since this type allows knowledge providers to find and use the context they need for representing at least one case when, where, ..., for whom, ... a relation is or is not true (and if they still do not know or do not want to deliver that information, using a context to state this ignorance or reluctance is also a way to comply with the specification even though this is not particularly interesting for the exploitation of the KB, hence its quality). Since complying with a universal completeness specification ensures that the number of relations with the specified relation types is maximal in the previously cited sense – i.e., the number of (positive or negated) (inferable or directly asserted) relations of the specified relation types cannot be augmented – a second conclusion is that, with the formal GKS viewpoint, universal completeness specification is a guarantee of the maximal quality of the KB wrt. its specified relation types (hence, complying with it is relevant if complying with its existential completeness counterpart is relevant).
• Some ontologies are not built or reused for general knowledge sharing, retrieval or exploitation but only for a particular knowledge-based application only. Hence, these ontologies may not be designed according to the formal GKS viewpoint. In this case, because of operational constraints (e.g. efficiency and memory constraints), the statement “the more constrained the definitions (or, the more a KB has relations from an object to other objects), the better” is not true. However, the designer of such an “operational ontology” may want to reuse existing ontologies and filter out some of their relations (as above noted). Thus, for selecting such ontologies, this designer may adopt the formal GKS viewpoint. Conversely, this viewpoint may also be adopted to check the quality of an operational ontology for GKS purposes. To conclude, the relevancy of using a universal completeness specification to evaluate a KB is related to how this KB is (re-)used. However, when the formal GKS viewpoint is adopted, complying with a universal completeness specification is relevant when complying with its existential completeness counterpart is relevant.

Three advantages of the above universal completeness specification example, at least from the formal GKS viewpoint. These advantages are related to the fact that, in a KB complying with this specification, the number of relations with the specified relation types is, in the above cited sense, maximal.

• Using the “closed-world assumption” (i.e., any statement not represented in the KB is assumed to be false) and the “unique name assumption” (i.e., different identifiers are assumed to refer to different things) do not lead to any more inferences regarding relations of the three above cited types. In other words, at least wrt. these relations, the KB supports these inferences without having to make these assumptions.
• Many modelling problems are not detected without the systematic (direct or inferred) connection of any two classes by (positive or negated) relations of the three above cited types. A first example is the case of unwanted cycles of rdfs:subClassOf relations (such cycles are made possible by the fact that rdfs:subClassOf is not a strict subclass relation type). A second example is the case of oversights or misinterpretations of the exact meanings of classes, typically illustrated by shared subtypes or instances to exclusive classes, such as to i) a class referring to the notion of representation as the act of representing, and to ii) a class referring to the notion of representation as a description resulting from the act of representing. A third example is the categorization of identical or similar classes at very different places in an ontology, without equivalence or subclass relation to relate them.
• Classes – and then, via them, their instances – can always be compared – and thereby also searched by query or navigation – i) via their subtype relations, but also ii) via their exclusion relations. This second possibility is less classic but also useful. As an example, it should first be noted “sports halls” would typically not be categorized as “lodging” (at least in ontologies for particular applications) but, from a formal GKS viewpoint, these two notions should be represented as not exclusive since “sports halls” are often used as “temporary emergency lodging” in case of natural disasters. (The exclusive notions of “emergency lodging” and “classic lodging” may then be represented. For simplicity purposes, a particular application may choose to refer to a “classic lodging” as a “lodging”.) It should be noted that it is easier to represent such non-exclusion relations than to create classes such as “temporary emergency lodging” and then represent all their possible subclasses. Using such non-exclusion relations are also more reusable for other purposes. No claim is here made about a benefit of exclusion relations for efficiency purposes or, more generally, for operational purposes.

This above universal completeness specification example – and its advantages – can be generalized to all types: C%( {every sub:Type}, {sub:supertype, sub:equivalent_type, sub:exclusive_type} ). This specification can similarly be adapted to check the organization of statements (instead of types) via generalization, equivalence and exclusion relations. Section 5.2.4 illustrates this point and its advantages.

/* Reminder: texts in “olive” color are not planned to be included into a journal article version because some reviewers may find these texts too complex. This is why, like this paragraph, the last sentence of the previous paragraph refers to Section 5.2.4. */
Universal completeness wrt. implication, equivalence and exclusion between statements (i.e., non-empty sets of relations). With “=>!” (alias, “=>¬”) referring to the type of “exclusion between two statements” derived from “=>”, C%( {every sub:Named_statement}, {=>, <=>, =>!} ) is analogue to the previous specification but applies to named statements, i.e., those that have been reified and named. Since naming statements can be cumbersome, the next specification may be more advantageous: C%( {every sub:Statement_for_inferences}, {=>, <=>, =>!}, {ic:Every-object_to_every-object, Destinations_in_the_source-object-set} ). The type sub:Statement_for_inferences refers to all the largest connected graphs of asserted relations that i) can match the premises of at least one user-provided “=>” relation in the KB, and ii) include each of the parts that would make them false if removed (e.g., each contextualization and OR part). For the destination objects to be of type sub:Statement_for_inferences too, the default ic:Every-object_to_every-named-object is replaced by ic:Every-object_to_every-object and Destinations_in_the_source-object-set. If a KB fully complies with one of the above two specifications, all the specified statements are organized via positive or contextualized “=>” relations (that are manually set or that can be deduced by the inference engine) into (or wrt. objects in) a “=>” hierarchy where objects are also connected by equivalence and exclusion relations, whenever possible. These relations can be deduced by the used inference engine if the types of the KB comply with the last specification of the previous paragraph, and if the used inference engine can fully exploit the content of the statements (this implies that this content is fully formal and that the used logic is decidable). This hierarchy may be useful for performance or explanatory purposes. As explained in the last paragraph of Section 5.2.4, this previous specification may also be extended and exploited by the editing protocol of a shared KB for enabling its users to cooperatively update it while keeping it free of inconsistencies or redundancies, without restricting what the users can enter nor forcing them to agree on terminology or beliefs. Note: C%( {every sub:Statement_for_inferences}, {=>}, {ic:Only_positive-relations_may_be_checked} ) might be viewed as one possible measure for the consistency of a KB. With classical logics, the result is either 0% or 100%, and it is the same with some other cardinalities (e.g., ic:Every-object_to_every-object, ic:Every-object_to_some-object or Some-object-to-some-other-object). With paraconsistent logics, the result is not “either 0% or 100%”.

Some advantages of existential/universal completeness for checking software code or the organization of software libraries. Some software checking approaches exploit relations between software objects (such as functions, instructions and variables), e.g. partOf relations, generalization relations and input/output relations. Such relations are stored into graphs (often called “Program Dependence Graphs” [Hammer & Snelting, 2009] [Zhioua, 2017]) and may for example be created by automatic extraction from software code (e.g., as in Information Flow Control techniques) or by models in approaches based on model-driven engineering. Using completeness checking functions on such graphs seems interesting. Here are two examples.

• C%( {every sub:Function}, {sub:precondition, sub:postcondition, sub:annotation}, {ic:Every-object_to_some-object} ) permits to know the percentage of functions (in the checked program or software library) that have preconditions, postconditions and/or annotations storing KRs about the function.
• Similarly, when applied to a graph representing a library of software components, C%( {every sub:Function_or_function-description}, {sub:function_generalization, sub:function_equivalence, sub:function_part, sub:function_successor_in_the_control_flow}, {ic:Every-object_to_every-object} ) returns 100% if every pair of function descriptions is connected by positive relations of the specified types. The expression “function descriptions“ is used for not only referring to “(types or definitions for) functions“ but also to logical or informal descriptions that refer to or generalize these functions. In a library, these descriptions may be in different formal or informal languages but the previous specification mandates their organization by transitive relations of the five cited types. Via sub:function_part relation, this organization also includes each structural relation between a function and the ones it may call according to its function body. Functions are also connected to their outputs or inputs (which themselves may be functions), and them to their types. To sum up, this organization represents the most common and important dependencies or relationships that can exist between software objects or descriptions of them, thereby reducing implicit redundancies between them, and increasing the possibilities to use conceptual queries for retrieving or checking them.

Proposal of default values for completeness specifications and list of the ones used in this article. The examples in this article show that some kinds of completeness specifications are more powerful or seem more often useful than others, hence more interesting to choose as default values. E.g., as above shown, at least from a formal GKS viewpoint, a specification with ic:Every-object_to_every-object seems more powerful and interesting than the same one with ic:Every-object_to_some-object. Indeed, creating a KB complying with the first specification i) implies creating a KB complying with the second, and ii) as above illustrated, this maximizes the number of relations of the specified types (thus maximizes inferences wrt. these types) without having to represent many more relations or, at least, without having to represent all that the negated relations that the the inference engine can deduce (typically based on relation signatures, exclusion relations, subtype relations and instance relations). Even in the previous paragraph – which uses ic:Every-object_to_some-object if only because this is more intuitively understandable – ic:Every-object_to_every-object could be used instead: this would lead to the creation of a well organized library with only well-organized data types and functions that allow type inferences (such as those made by interpreters or compilers of functional programming languages), if only to avoid having to manually represent too many relations. However, as above explained, a specification with ic:Every-object_to_every-named-object seems generally more interesting to use than the same one with the less restrictive ic:Every-object_to_some-object. Thus, to collect the choices of default values used in this article: i) the set of relation destination is by default the whole KB (the signatures of the relation types that can be specified via the 2^nd parameters, as well as the constraints that can for example be made via the 3^rd parameters, seem sufficient), ii) sets are by default AND-sets, iii) ic:Every-object_to_every-named-object and ic:The_checked-relations_may_be_negated-or-otherwise-contextualized are default values in the 3^rd parameter and hence may be left implicit.

2.5. Comparison of The General Approach With Some Other Approaches or Works

The introduction distinguishes intrinsic completeness measures from extrinsic completeness ones or other KB quality measures. Compared to other approaches – e.g. classic constraint-languages, the use of axioms and predefined measures – the introduction also highlights the original features of the presented general approach: it exploits the start of ontology about intrinsic completeness centered around some generic functions which can exploit other types defined in this ontology and the implication operator of the inference engine selected by the user. Thus, the approach has the originality of allowing its users (the users of its functions) to create quite expressive and concise intrinsic completeness specifications tailored to their KB evaluation needs, while writing parameters with the KRL they wish to use. Conversely, this ontology – and hence approach – could be reused in some constraint-languages or query languages to allow their users to write more concise and expressive intrinsic completeness specifications, and then check a KB wrt. these specifications. The next subsection (section 2.6) provides an overview of the content of the ontology. Section 2.7 shows how the ontology categorizes types that permit the representation of common criteria or best practices that can be related to intrinsic completeness, and thus is another kind of comparison of the present work with other ones. Since the other existing KB quality measures or checking tools are predefined, the rest of this subsection shows how those that can be related to intrinsic completeness can be represented with the introduced approach. This is also a kind of comparison with these predefined measures.

Specification of most of the checks made by Oops! The ontology checking tool Oops! [Poveda-Villalón et al., 2014]) proposes a list of 41 “common pitfalls”. These semantic or lexical errors are grouped according to four non-exclusive “ontology quality dimensions: Modelling issues, Human understanding, Logical consistency and Real world representation”. Oops! can automatically check 33 of them. Out of these 33, it seems that i) 16 are about missing values or relations which could be prevented by specifications represented via OWL definitions or SHACL (Shapes Constraint Language) [Knublauch & Kontokostas, 2017], and ii) 9 are inconsistency problems which could often be prevented by specifications represented via OWL definitions (and an inference engine exploiting them). The 8 remaining problems are more lexical (and related to names or annotations) or related to i) the non-existence of files or objects within them, or ii) normalization (“P25: Defining a relationship as inverse to itself”). The 16 pitfalls about missing values or relations can be detected via intrinsic completeness specifications. (These problems may also be detected via OWL definitions, which seems preferable since definitions are knowledge representations which are important not just for checking purposes). E.g.:

• A formalization of a specification detecting the “Modelling issue” pitfall named “P4: Creating unconnected ontology elements” is CN( {every owl:Thing}, {sub:relation}, ic:Every-object_to_every-named-object). Similarly, “P11: Missing domain or range in properties” can be detected via CN( {every rdf:Property}, {rdfs:domain, rdfs:range}, ic:Every-object_to_some-object ). “P13: Missing inverse relationships” (later renamed “Inverse relationships not explicitly declared”) can be detected via CN( {every rdf:Property}, {owl:inverseOf}, ic:Every-object_to_some-object). Although [Poveda-Villalón et al., 2014] does not mention meta-statements, occurrences of these pitfalls remain problems when meta-statements are used on these occurrences (this remark is essentially for the pitfall P4 since it is most unlikely that meta-statements would be used in occurrences of the pitfalls P11 and P13). Thus, the use of the type ic:The_checked-relations_may_be_negated-or-otherwise-contextualized as a default value in the 3^rd parameter is here again relevant.
• The “P6. Including cycles in a class hierarchy” pitfall (categorized as both a “Logical consistency” and a “Modelling issues” problem) is prevented by complying with C%( {every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass}, {ic:Every-object_to_every-named-object, ic:The_checked-relations_may_be_negated} ). Indeed: i) these cycles imply that the connected classes are equivalent (these cycles are allowed by the fact that rdfs:subClassOf relations are not strict, i.e., rdfs:subClassOf can be seen as a subtype of owl:equivalentClass), ii) this last specification asks for the classes to be related by a positive owl:equivalentClass relation or a negated one (e.g., via the use of a relation of type sub:non-equivalent_class, as noted in Section 2.4), and iii) when two classes are stated as both equivalent and non-equivalent, many inference engines can then detect an inconsistency (e.g., inference engines that can handle OWL, if the statements directly or indirectly use OWL types).
• The “Modelling issues” pitfall named “P10. Missing disjointness” is about whether “The ontology lacks disjoint axioms between classes or between properties that should be defined as disjoint”. As shown by Section 2.4, whether an ontology “lacks disjoint axioms“ may be seen as application dependent but, with the formal GKS viewpoint, the following formalization is relevant for P10, P6 and more: C%( {every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass, owl:disjointWith}, {ic:Every-object_to_every-named-object, ic:The_checked-relations_may_be_negated-or-otherwise-contextualized} ).

/* The rest of this section is to be rewritten based on the parts below */

“Coverage of a class” in the sense used in [Karanth & Mahesh, 2016]. In [Karanth & Mahesh, 2016] (unlike in [Duan et al., 2011]), the “coverage” of a class in a KB is the ratio of i) the number of instances of this class, to ii) the number of instances (in the KB). For a class identified by C1, such a coverage could be measured via C%( {every owl:Thing}, {rdf:type ---> Cl}, {ic:Every-object_to_some-object, ic:Only_positive-relations_may_be_checked} ): due to the cardinalities ic:Every-object_to_some-object in the 3^rd parameter, this call returns 100% if and only if every object of type owl:Thing (e.g. a class if there are meta-classes) is source of some (i.e., at least one) rdf:type relation to Cl. This relation must be positive due to the restriction ic:Only_positive-relations_may_be_checked. This restriction could also be written as [any sub:Statement ––ic:contextualizing-relation-type_taken-into-account––> {}] which can be read: “any statement has for ic:contextualizing-relation-type_taken-into-account an empty set of types” (thus, no contextualized statement can be counted as complying with a specification).
Similarly, for a property identified by p, a derived kind of coverage could be measured via C%( {every owl:Thing}, {p}, {ic:Every-object_to_some-object, ic:Only_positive-relations_may_be_checked} ). Above, every owl:Thing refers to every object in the KB (including types and statements) since the specifications do not state i) any restriction about where the sources of the selected relations come from, nor ii) that the query should only apply to individuals.

“Domain/range coverage of a property” in the sense used in [Karanth & Mahesh, 2016]. In [Karanth & Mahesh, 2016], the “domain coverage” of a property p (in a KB) is the ratio of i) the number of instances source of a p relation, to ii) the number of instances having a type that belongs to the domain of p. Assuming that instances source of a p relation have a type belonging to the domain of p, such a coverage could be measured via C%( {every ^(rdfs:Class<--rdfs:domain--p)}, {p}, {ic:Every-object_to_some-object, ic:Only_positive-relations_may_be_checked} ). This call returns 100% if every “instance of a class that is destination of an rdfs:domain relation from p” is source of a p relation. Indeed, in the used notation, “^(...)” allows the definition of an anonymous type.
Similarly, the “range coverage” (of a property p, in a KB) from [Karanth & Mahesh, 2016] can be measured via C%( {every ^(rdfs:Class<--rdfs:range--p)}, {p}, {ic:Every-object_to_some-object, ic:Only_positive-relations_may_be_checked} ).

Comparison to the measure named “coverage” in [Duan et al., 2011] (this paragraph reuses some parts of Section 2.4.3). In [Duan et al., 2011], the “coverage of a class within a dataset” is with respect to the “properties that belong to the class”. For each of these properties (binary relations from the class), this coverage is (very informally) the ratio of i) the number of occurrences of this property in (all) the instances of this class, to ii) the product of “the number of properties in this class” and “the number of instances of this class (in the evaluated dataset)”. This coverage was designed to return 100% when all instances of a class have all the “properties that belong to the class” (to use the terminology of [Duan et al., 2011], one more often associated to some frame-based KRLs than to more expressive KRLs). To represent and generalize this last expression, C* and its derived functions can exploit the special variable (or keyword) “$each_applicable_relation” in their 2^nd parameter. This variable specifies that “each relation type (declared in the KB or KBs it imports) which can be used (e.g., given its definition or signature) should be used whenever possible, directly or via a subtype”. E.g., for a class identified by Cl, a call to C%( {every Cl}, {$each_applicable_relation}, {ic:Every-object_to_some-object} ) would return the ratio of i) the number of instances of Cl that have at least one relation of each of the possible types, to ii) the number of instances of Cl. Thus, 100% would be returned when all instances of Cl have (at least one instance of each of) all the relations they can have. This is not the measure of coverage described in [Duan et al., 2011] but has a similar intent and is compatible with more expressive KRLs. To compare KBs, [Duan et al., 2011] advocates the use of the “coherence of a class within a dataset”; it is the sum of a weighted average of the coverages of the classes, thus not a ratio between comparable quantities and not a particularly intuitive measure. With C%, comparing KBs based on similar coverages of their classes could instead be done by calling C%( {every rdfs:Class}, {$each_applicable_relation}, {ic:Every-object_to_some-object} ) for each KB and then comparing the results. The above described coverage measure is also not a ratio between comparable quantities. In that respect (among others), it is similar to the “relationship richness of an ontology” measure of OntoQA [Tartir et al., 2005]: it is the number R of “defined relations from an instance of a class“ divided by the sum of R and the number of subclass relations. [Vrandečić, 2010] shows that such measure is “pretty much meaningless” (Section 6.1.3) and, as a preferred “repair” (while keeping a similar intent), proposes the following formula: the number of relation types R2 divided by the sum of R2 and the number of classes (Section 8.4). This new formula divides a number of types by another number of types.

Conclusion wrt. KB evaluation measures. Current KB evaluation measures that can be categorized as intrinsic completeness measures have far fewer parameters and do not exploit contextualizations. Thus, they do not answer the research questions of this article and, unlike KB design recommendations, can rarely be extended to exploit aboutness. Many of such measures also rely on statistics that are not simple ratios between comparable quantities (quantities of the same nature), and thus are often more difficult to interpret. All these points are illustrated near the end of Section 2.2 (Comparison to the measure named “coverage” in [Duan et al., 2011]). In [Zaveri et al., 2016] (and [Wilson et al., 2022]), “coverage” is an extrinsic completeness measure since it refers to the number of objects and properties that are necessary in the evaluated KB for it to be “appropriate for a particular task“.

Formalizing, Categorizing and Generalizing KB Design Recommendations
OLD (was hidden) TO RE-USE HERE? : Extending KB design recommendations, capturing more knowledge, supporting more inferences. Most KB design recommendations do not mention the possibility of using negations or other ways to state something about particular recommended relations. The above described approach permits the extension of KB design recommendations with this possibility. With it, what is now “recommended” is to represent knowledge in such a way that the truth status or conditions of particular relations can be inferred by the used inference engine. Thus, this approach answers the second and third research questions listed in the introduction: the representation of knowledge – and the extension of KB design recommendations – for supporting “the automatic checking that relations of particular types are systematically used but only when the setting of these relations is considered correct by the knowledge provider (not simply whenever this use is allowed by the relation signatures, for example)”. /* no: makes them more applicable since the knowledge providers may do not just have to assert the recommended relations, they may also state when they are false or the conditions for their truth */ This approach also encourages the representation of more knowledge (e.g., negated relations) and thereby leads to the creation of KBs supporting more inferences.
Conversely, the more the statements required by a specification can be inferred, the easier it is to build a compliant KB. Thus, the more precise the definitions associated to the types of the evaluated relations (e.g., regarding their signatures and cardinalities), the more general the classes they are associated to, and the more organized the ontology (at least by subtype and exclusion relations), the more the statements required by a specification can be inferred. E.g., when an object has a functional relation (e.g. an instance of owl:FunctionalProperty), the inference engine knows that it cannot have relations of the same type to other objects. /* Thus, as later illustrated, complying with this KB design recommendation is not necessarily difficult. */
Current KB evaluation measures that can be categorized as intrinsic completeness measures do not take into account contextualizations/* aboutness related representations*/. Thus, they do not answer the research questions of this article and, unlike KB design recommendations, can rarely be extended to that end. Many of such measures also rely on statistics that are not simple ratios between comparable quantities. Thus, their results are also often more difficult to interpret.

2.6. Overview of Important Kinds of Parameter Values Via a Simple User Interface

/* This section is to be partially rewritten based on the parts below */

Quick explanation of the interface. Figure 1 shows a simple graphic user interface for i) helping people build parameters for some functions like C%, ii) generating a query (function or SPARQL query) or, in some cases, a SHACL constraint, and iii) calling a KB server (e.g. a SPARQL endpoint) with the query or constraint. This server displays the results of the execution of the query or of the adding of the constraint. Since KB servers rarely accept the uploading of a KB into them, no menu is proposed for that in this interface. For functions, this interface was tested with WebKB-2; for SPARQL+OWL or SHACL, a local Corese server was used. Each of the points below comments on one menu of the interface. These points are only meant to give an overview and general ideas about what can be achieved. In these menus, the indentations always represent specializations.

• The “Level” menu on the top right corner selects options in the four selection menus about the parameters: those in the middle of Figure 1. This figure shows the selection of the options for the level named “Good (/ Owl+Sub)”. OWL-RL or OWL-QL, along with some Sub relations defined with these OWL profiles, are sufficient for class definitions to fully comply with the options of this level and to check this compliance (but this is often not the case for relation type definitions, statements and individuals). (Section 3.1.1 gives more details for type definitions).
• The “From such objects” menu enables the selection of some particular types and quantifiers for the 1st parameter of C* (thus, this menu is in the 1st column), hence for the objects in the sources of relations selected to be checked.
• The “To such objects” menu is related to the 3rd parameter of C* but had to be placed in the 1st column of Figure 1. It is about where the destinations of the selected relations may come from, in relation to the “to” part of cardinalities. It is essentially useful for universal completeness (in other words, it is rarely useful for existential completeness). The “accessible objects” option refers to the following of relations across KBs (hence, in the RDF world, by “dereferencing URLs“). This option can be implemented via the SPARQL of Corese but not via SPARQL 1.1. The rest of Section 2.4 discusses the options in this 3^rd parameter that have not yet been introduced, their interest and the extent to which they can be taken into account with SPARQL and OWL.
• The “Via ... relations of these types” menu shows particularly interesting types (of possibly contextualized or deducible relations) to be checked. The “sub:” prefix is not displayed. This interface only proposes relation types such as the ones previously defined or other primitive ones such as sub:partOf. Section 4 and Section 5 explain the relations types that have not yet been introduced, the interest of using them in the 2^nd parameter, and shows the extent to which they can be taken into account with an implementation of CN, CN– or C% that uses SPARQL and OWL.
• Most of the options shown in the “Other checked constraints” menu are related to the 3rd parameter of C*. Section 2.4.5 shows how a universal completeness specification with the “minimal differentia (between any two selected objects)” option is a way to define, extend and implement the “Differential Semantics” methodology of [Bachimont, Isaac & Troncy, 2002], itself an extension of the genus & differentia design pattern. E.g., a SPARQL query is proposed as one way to implement it via CN–. Similar options are proposed to obtain other particular structures for the organization of “==>” relations and to sub:part relations in a KB. Other options in this menu are about previously explained kinds of parameters (e.g., what is above called “cardinalities”). The displayed options that have not yet been mentioned will be explained by the end of this article.

Figure 1. A simple interface for the evaluation of intrinsic completeness with respect to
logical or primitive relation types, and via CN, CN– or C%

Intrinsic Completeness Via Logical/Primitive Relation Types CN: number of compliant selected source objects CN–: list of non-compliant objects C%: CN / number of selected objects Cr%avg: average of compliant relations from&to the selected objects CNr–: list of non compliant relations from&to the selected objects CNr: number of compliant relations from&to the selected objects Cr%: CNr / number of relations from the selected objects   Level: Strict minimal Ok; needs only Owl Good (/ Owl+Sub)Better (/ Owl+Sub) From such objects   Thing   //-> any object   Type   //-> types only      Class      Property   Individual      Statement      Non-stmt_indiv   *   //any quantification   ∀   ∃    To such objects    for all kinds of            cardinalities    for the "every to every"            kinds of cardinalities accessible objects     in the KB         in the source set         last added object Via positive/negated/contextualized/...  relations of these types relation   $each_applicable_relation   type   partOf   //alias, superPart   part_exclusion   ==>*   //groups next subtypes:        ==>              <==>                  equivalent_class                  equivalent_property              "==>  ∩  !<==>"                  strict_superClass                  strict_superProperty                  def_necessary-element        ==>!   //alias, ==>_exclusion              disjoint_class              disjoint_property        ==>-element        ==>-element_exclusion   definition-element_exclusion   definition-element   elementOf-==>   elementOf-==>_exclusion Other checked constraints every object to some object   every object to some other object every object to every object   every object to every named object   *  →  *   //no enforced quantification   ∀:every/any/anyByDefault  →  *   *  →  1..* complete{...}   *  →  1..* exclusive{...}      *  →  1..* partition{...}   minimal differentia   shared genus wrt. "==>" relations   shared genus+exclusionSet     "==>" tree structure   "==>" join-semilattice structure   shared genus wrt. partOf relations   shared partOf genus+exclusionSet     partOf tree structure   partOf join-semilattice structure   relation_modifier   not   contextualizing-relation Below is a manually updatable  (generated from the above menus)  query constraint   in   FL (→ as a function) SPARQL    C%( { every owl:Thing }, //+: by default, source objects may have "any quantification" { $each_applicable_relation, rdf:type, sub:==>, sub:<==>, sub:def_necessary-element, sub:==>!, sub:definition-element_exclusion }, { //by default: "*", "in the KB", ic:Every-object_to_every-named-object, "* → *" "minimal differentia", "shared genus+exclusionSet" } )   to the knowledge server at

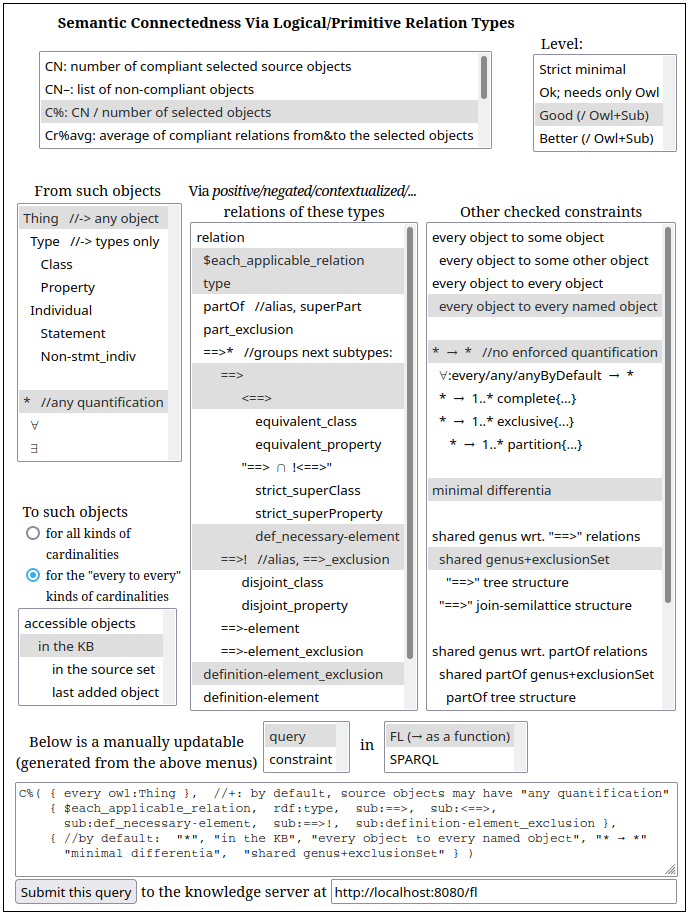
2.7. Ontology of Operators, Common Criteria or Best Practices Related to Intrinsic Completeness

2.7.1 Ontology of Operators Related to Intrinsic Completeness

/* This section is to be written - or removed - based on the parts below */

Intrinsic completeness of a unique object (instead of a KB). This notion might seem counter-intuitive at first but is naturally derived by restricting the 1^st parameter set of C% to only one particular object, e.g. by explicitly giving its identifier (the simple selection menus of Figure 1 do not support the use of such an identification).

CNΔ (relation usefulness). CN( {every sub:Statement_for_inferences}, {=>, <=>, =>!}, {ic:Every-object_to_every-object, Destinations_in_the_source-object-set} ) gives the number of “statements for inferences” related by positive or contextualized relations of the three indicated types. This number may be seen as indicating the number of inferences (based on these types) between such statements in the KB. This number can be obtained right before and right after a relation is added to the KB – added explicitly, as opposed to inferred. CNΔ, the difference between the two obtained numbers, is the number of additional inferences (of the cited kinds) that this added relation has led to. More formally, in a (portion of) KB that is identified as Kb and that does not yet include a particular relation “r”:     CNΔ(r) =def  CN(Kb ∪ r, {=>, <=>, =>!}) – CN(Kb, {=>, <=>, =>!})

2.7.2. Categorization of Common Criteria or Best Practices For KB Quality

/* This section is to be written (or removed) based on the parts below */

Box 1 shows that common criteria or best practices (BPs) for the quality of KBs can often be categorized as intrinsic completeness ones. For each such criteria or BP, the types of the exploited relations depend on the used particular implementation, and the ontologies they come from but. However, assuming that these ontologies are aligned, a specialization hierarchy of these implementations could be derived. Each implementation would also depends on the used underlying approach – e.g., the one explored in this article – and the used implementation language.

Relying on objects from an external dataset (e.g. one for a domain or a task):
  P+Z:Relevancy, P:Understandability, Z:Semantic_accuracy, Z:Interoperability
  P+Z:Completeness (P:Intensional/Extensional/LDS, Z:Schema/Property/Population/Interlinking)
Intrinsic (i.e. not using an external dataset as a model):
  Lexical, syntactic or structural (→ not exploiting semantic relations; in the referenced surveys, 
        the descriptions of the following criteria seem to refer only to lexical, syntactic or
        structural features but these criteria could be generalized to cover semantic features too):
    Z:Security (P:Verifiability (P:Traceability, P:Provability, P:Accountability)),
    P+Z:Syntactic_validity, P+Z:Interpretability, P+Z:Understandability, Z:Versatility, M:Richness,
    Z:Representational-conciseness, Z:Performance
  Semantic (→ exploiting semantic relations, hence INTRINSIC COMPLETENESS criteria or BPs):
    About metadata (relations to names or definitions are not considered as metadata):
      About licences: Z:Licensing, P:Openness, F:DataLicense, F:FollowLicensingTerms
      Not about licences: F:VersioningInfo, F:VersionHistory, F:VersioningPolicy,
        F:ProvideMetadata, F:DescriptiveMetadata, F:StructuralMetadata, F:DataProvenance,
        F:DataQuality, F:DataUnavailabilityReference, F:documentYourAPI,
        F:FeedbackInformation, F:ProvideFeedbackToPublisher, F:CiteOriginalPublication,
    Not about metadata (but possibly related to names and definitions):
      Solely about names: "Give each resource a URI and names in various languages"  [w3c, 2014d]
      Solely about definitions (formal or infomal ones): M:Clarity,
        "give each type an informal definition in various languages" [w3c, 2014d]
      P+Z:Consistency, Z:Semantic_accuracy, Z:Conciseness, P:Structuredness (P:coverage),
      M:Cohesion, M:Coupling, M:Deployability, M:Expandability, M:Adaptability, M:Sensitiveness,
      P:Reachability, Z:Interoperability, Z:Interlinking,
      Z:Trustworthiness, Z:Availability, F:DataUnavailabilityReference, 
      P+Z:Timeliness (P:Newness, P:Freshness)

2.8. Evaluation of the General Approach Wrt. Subtype Or Exclusion Relations In Some Foundational Ontologies

/* This section is to be fully rewritten based on various top-level ontology evaluations (such as the one described below) and the use of C%% too for these evaluations. A table will compare the results for the various ontologies. */

Evaluation of a well known foundational ontology (this paragraph is a summary of Section 3.1). To illustrate one experimental implementation and validation of this approach, DOLCE+DnS Ultralite (DUL) [Gangemi, 2019] – one of the most used foundational ontologies and one represented in RDF+OWL – has been checked via C%( {every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass, owl:disjointWith} ). More precisely, an automatic check was made on an extension of this ontology (“DUL 3.32 + D0 1.2” from the same author; version of April 14th, 2019) but it is still named DUL below. For understandability and analysis purposes, [Martin, 2020] gives an FL-based and modularized very slight extension of this ontology. The first result was 0%: no DUL class has a positive/contextualized asserted/inferable relation to every class for each of the above listed types. Partial reasons for this are: i) DUL uses rdfs:subClassOf instead of a strict subclassOf relation, and ii) it has few owl:disjointWith relations. However, only a few exclusion relations had to be added to DUL for the following assumption to be true: no class is equivalent to any other class and no class has other potential supertypes, subtypes and exclusions than those explicitly represented. Then, for making this explicit – i.e, for this assumption to be unneeded – the rdfs:subClassOf relations were replaced by more precise ones (typically of the above cited sub:sC type); this made the modified version of DUL automatically checkable via the above cited C% call and then the result was 100%. Given the names and comments associated to DUL classes, the relations added for making the above assumption true seemed warranted. For DUL, with some weaker assumptions, the maximum result was 11.9% (more precisely 10/84). Details are given in Section 3.1. The organization of relation types has been similarly checked via C%( {every rdf:Property}, {rdfs:subPropertyOf, owl:equivalentProperty, owl:propertyDisjointWith} ). The results were also 0% when no assumption was made and 100% (more precisely, 112/112) when the above cited one was made. However, to make this assumption true, a lot of seemingly warranted exclusion relations and non-exclusion relations had to be added between the relation types. Some other top-level ontologies were similarly checked and the results were similar. This is not surprising: nowadays, even in top-level ontologies, it is rare that subtype partitions or sets of exclusive subtypes are used whenever possible (and, it is even rarer that non-exclusion relations are set for making explicit to the inference engine that some types cannot be related by exclusion relations). Nevertheless, as earlier noted, in the general case, adding such relations is easy and support inferences that may prove valuable for some applications (this does not mean that, for most current applications, such relations would lead to better results or a better performance).

DOLCE+DnS Ultralite (DUL) [Gangemi, 2019] is one of the best known – or most used – foundational ontologies and is fully represented in OWL. This section reports and analyses some intrinsic completeness measures of a slight extension of this ontology (DUL+D0, from the same author) and, more precisely, its last version in April 2020 (D0 1.2 + DUL 3.32; OWL/Turtle versions of April 14th, 2019). For understandability and analysis purposes, an FL-based and modularized slight extension has also been made [Martin, 2020].

DUL+D0 has 84 classes and 112 relation types. The classes have for uppermost type dul:Entity and are well organized by subtype and exclusion relations: 8 classes are at a subtype depth of 8 (and 2 classes are at a subtype depth of 9) and 89% of classes are source of at least one exclusion relation. The relation types have for uppermost type dul:associatedWith and are not so organized: there are no exclusion relation between them and 8 of them are at a subtype depth of 3, the maximal depth.

For DUL+D0, without making any assumption, C%( {every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass, owl:disjointWith} ) – a specialization of C%( {every rdfs:Class}, {==>, <==>, ==>!} ) – returns 0%: no class has a positive/negative direct/inferred relation to every class for each of the above listed types (and the result is the same without owl:disjointWith in the 2^nd parameter). One reason is that DUL+D0 uses rdfs:subClassOf instead of sub:proper-subClassOf (or any equivalent or more precise relation type): many classes are not connected by relations stating that these classes are not equivalent and thereby no class is explicitly non-equivalent (and thereby different) to all other classes; thus, some inference possibilities are lost.

Given the names and informal definitions of the types in DUL+D0, it is clear that all its subtype relations are meant to be strict. With that first interpretation assumption, the result is 1/84 instead of 0%: only dul:Entity is related to every class in the specified ways. One reason is that many classes are still not connected by relations that make these classes non-equivalent since i) DUL+D0 uses rdfs:subClassOf instead of a subtype of sub:proper-subClassOf which, like sub:sC (cf. Section 3.1.2), is defined to imply that the subclass is uncomparable to its siblings, hence non-equivalent to them, and ii) not all siblings, i.e. not all direct subclasses of a same class, are related by exclusion relations (this would imply that they are non-equivalent).

However, another interesting and rather safe interpretation assumption for rdfs:subClassOf is that it introduces a subclass that is not only non-equivalent to its siblings but actually “uncomparable and non-exclusive with these siblings as well as with the supertypes and subtypes of these siblings, unless there is a statement (typically an exclusion relation) that permits the used inference engine to infer otherwise”. This assumption is correct for DUL+D0. With that additional assumption, the result is now 10/84 instead of 1/84. The result is 10/84 whether or not owl:disjointWith is in the 2^nd parameter since i) owl:disjointWith relations are derived via the assumption whether or not they are taken into account by the evaluation, and hence ii) the non-equivalence relations which are inferred from the owl:disjointWith relations are taken into account in both cases. When building an ontology, it is better not to rely on assumptions. Hence, it is better to make the uncomparabilities and exclusions explicit. To that end, instead of creating subclasses by directly using rdfs:subClassOf, it is better to create “sets of subclasses” (and, whenever possible, at least one set of exclusive subclasses) via relations such as sub:sC relations.

• This is an easier method: as illustrated in Section 3.1.2) where sub:sC is also defined, sub:sC is a shortcut for creating many relations. In Section 3.1.2, the SPARQL update operation associated to sub:sC replaces sub:sC relations by i) sub:proper-subClassOf relations, and ii) the siblings that are neither comparable nor exclusive are connected by sub:uncomparable-but-not-disjoint_class relations.
• This is a safer method: since relations of types such as sub:sC, along with relations of type such as owl:disjointUnionOf, offer a concise way to represent many relations, it is easier for the knowledge provider to quickly see all these relations and hence not to forget some of them. The FL notation provides even more concise variants of sub:sC and owl:disjointUnionOf relations. Thus, this method was used when making the above cited FL-based and modularized slight extension of DUL+D0 [Martin, 2020]. This led to the discovery that at least a dozen direct exclusion relations were missing (and that some explicit non-exclusion relations would have strongly helped understanding whether some other classes were exclusive).

A third and more risky interpretation assumption for rdfs:subClassOf is that it introduces a subclass that is “uncomparable and non-exclusive with any other type reachable via a chain of subtype or subtypeOf relations, unless there is a statement that permits the used inference engine to deduce otherwise”. This assumption is not fully correct in DUL+D0 because, as above noted, some exclusion relations are missing thus not preventing some incorrect interpretations. However, i) these missing relations are relatively rare compared to the number of relations (1393 inferable subclass relations and 4804 inferable oriented exclusion relations), and ii) not taking into account the consequences of these missing relations, this assumption is correct for DUL+D0. With this third assumption, the result is now 84/84. Without having to make assumptions, the result is the same if the missing exclusion and non-exclusion relations are specified, e.g. via the above mentioned method.

Similarly, regarding relation types in DUL+D0, C%( {every rdf:Property}, {rdfs:subPropertyOf, owl:equivalentProperty, owl:propertyDisjointWith} ) returns 0% when no assumption is made, 1/112 when the first assumption is made, 60/112 when the second one is made, and 112/112 when the third one is made. However, to make the last two assumptions correct, a lot of seemingly warranted exclusion relations (and non-exclusion relations) need to be added between these relation types.

Given the previous results, it did not seem necessary to show the results of an evaluation for another top-level ontology, nor for a general ontology such as DBpedia where there are relatively few exclusion relations. Indeed, the DBpedia of April 2020 included only 27 direct exclusion relations, 20 of them from the class named "Person" (this can be checked at http://live.dbpedia.org/sparql), while it included more than 5 million direct skos:broader relations.

3. Implementations Via a SPARQL Engine Exploiting an OWL Inference Engine

3.1. Exploiting OWL, SPARQL and SHACL For Checking Or Stating Relations Between Types

Rationale for checks via SPARQL or SHACL. Nowadays, many KBs are accessible to Web users via a SPARQL endpoint and sometimes only this way. Thus, for Web users that would like to check if a KB is sufficienty well-organized for being reused or for warranting further tests via a full download of the KB (using a static file or queries), issuing some SPARQL queries is interesting. Some KB developers also use SPARQL queries for some checks – e.g. the one of ontology patterns, as in [Sváb-Zamazal1, Scharffe & Svátek, 2009] – for example because the KRL they use is not powerful enough to represent these patterns in a way that support their checking or because the inference engine they use would not be powerful enough to exploit these ways. To support some checks, instead of using queries or adding knowledge to the KB, constraints can be represented (into the KB or, if a different language is used, in a separate file). For constraint, the W3C proposes the use of SHACL (Shapes Constraint Language) [Knublauch & Kontokostas, 2017].

Experimental validation via Corese. The SPARQL queries or operations – and SCHACL constraints – proposed in this section have been validated experimentally using Corese [Corby & Faron-Zucker, 2015], a tool which includes an OWL-RL inference engine, a SPARQL (1.1) engine, and a SHACL validator.

Assumption for all SPARQL queries in this article: only positive or negated relations are taken into account. In the rest of this article, the constraint “[any sub:Statement ––ic:contextualizing-relation-type_taken-into-account––> {sub:negation}]” (illustrated in Section 2.2) is a default constraint.

3.1.1. Using SPARQL Queries To Check Some OWL-RL/QL Relations Between Types

Rationale for such queries. Section 4 shows the interest that a KB has for inconsistencies and redundancies detection, search purposes and, more generally, inference purposes, if this KB is “universally complete wrt. implication, generalization, equivalence and exclusion relations” (i.e., if, for any pair of objects, the used inference engine knows whether one object has implication, generalization, equivalence or exclusion relations to the other, or the conditions when such relations exist, or if they cannot exist; the expresssion “universally complete wrt. some relations” was informally introduced by Section 2.2). The present section shows how such an intrinsic completeness can be a checked using SPARQL, with the following restriction: only “relations between types” from OWL-RL|QL (i.e., from OWL-RL or OWL-QL) are checked and hence only “universal completeness of types wrt. generalization, equivalence and exclusion relations”. Indeed, i) OWL is one de facto standard KRL model and, when an inference engine is used together with a SPARQL engine, it is most often an OWL engine, ii) OWL engines are often restricted to a particular OWL profile, typically OWL-RL, OWL-QL or OWL-EL, iii) OWL only provides generalisation types between types, not between statements, iv) allows one to express that a type is not subtype of another only via OWL-Full (which is not supported by current OWL engines) or by using a disjointness relation (i.e., by stating that a types cannot be subtype of another), and v) OWL-EL, the third common profile of OWL(2), does not support disjoint properties.

Query 1: implementation of CN–({every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass, owl:disjointWith}). In a KB without contextualization relation, this specification – which has no 3^rd parameter (hence which applies the “every object to every object” cardinalities) and uses CN–  – means “list every class related to every class by a relationship (i.e. a positive or negated relation) of type rdfs:subClassOf and a relationship of type owl:equivalentClass. The following SPARQL query implements this by

• searching all pair of classes (see the second line);
• discarding a pair of classes if they are connected by a direct OWL relation that asserts or negate a relation of type rdfs:subClassOf, owl:equivalentClass or owl:disjointWith, since those relations comply with the specified parameters and since CN– displays non-compliant object (see the third line; there is a partial redundancy in the checking here – but only a partial one – since relations of the last type already forbid the existence of relations of the first two types and hence, in a sense, negate them);
• also discarding a pair of classes if they are connected by an exclusion relation expressed via the use of owl:AllDisjointClasses (fourth line; if the SPARQL engine has an entailment regime that fully exploits an OWL-RL|QL inference engine, this fourth line is made redundant by the third line);
• also discarding a pair of classes if they are connected by an exclusion relation expressed via the use of owl:disjointUnionOf (fifth line); an OWL-RL|QL engine does not exploit this type when it is used in “a superclass expression” (i.e., when it is used for giving a subclass partition to a class) and thence does not derive exclusion relations between the subclasses; nevertheless, via this fifth line, these exclusion relations are still taken into account;
• displaying the remaining pairs of classes, i.e the ones not discarded by the “FILTER NOT EXISTS” expressions (first line).

Thus, this query checks all the ways a relation of type rdfs:subClassOf or owl:equivalentClass can be directly or indirectly asserted or negated with OWL.

Query 2: implementation of CN–({every rdfs:Class}, {rdfs:subClassOf, owl:equivalentClass}). Compared to the specification implemented by Query 1, there is one less property in the 2^nd parameter. Thus, here, the specification is relaxed, and hence less inferences are ensured (e.g., for search purposes and the detection of inconsistencies or redundancies). However, a KB complying with this relaxed specification still has the advantage that using the closed-world assumption or the unique name assumption does not lead to more inferences. The implementation of Query 2 is the same as for Query 1 except that one line is to be added at the end: “FILTER NOT EXISTS{ ?c1 sub:non-equivalent_class_nor_subClassOf ?c2 }”. This line discards a pair of classes if they are connected by a relation of type sub:non-equivalent_class_nor_subClassOf. Indeed, the parameters do not mandate anymore the two classes to be either disjoint or explicity not disjoint, they may now also be non-equivalent or one may be a subclass of the other. The above cited type is defined (using Turtle and OWL-RL|QL) as follows:
sub:non-equivalent_class_nor_subClass rdfs:range rdfs:Class ;
  owl:propertyDisjointWith owl:equivalentClass, rdfs:subClassOf .

Adaptations of the two previous queries for the “every object to some other object” and “every object to some object” kind of cardinalities. Below is the counterpart of Query 1 for the first of these two kinds of cardinalities – and, with the last “#” removed, the counterpart of Query 2 for the first kind. This implementation

• existentially quantifies “?c2” (variable for the destination class) by not binding it before its use in a “FILTER NOT EXISTS” expression, and
• checks that the relations with owl:Nothing as destination – those are relations generated by OWL engines, not important relations from a knowledge acquisition viewpoint – are not counted as relations complying with the parameters.

To obtain the counterpart of Query 1 for the second kinds of cardinalities, the “(?c1!=?c2) &&” expression in this query (the one in italics) must be removed. However, with this second kind and the given 2^nd parameter, no result is returned by CN– since every class is comparable to itself.

Query 3: implementation of CN–({every rdf:Property}, {rdfs:subPropertyOf, owl:equivalentProperty}). Below is the definition of sub:non-equivalent_property_nor_subPropertyOf in OWL-RL|QL, and then the adaptation of Query 2 for checking properties instead of classes. The kinds of explanations used for Query 1 and Query 2 also apply here; the difference is that OWL has no counterpart of owl:complementOf, owl:AllDisjointClasses and owl:disjointUnionOf for properties. Thus, to obtain the adaptation of Query 1 for property, i.e., to implement CN–({every rdf:Property}, {rdfs:subPropertyOf, owl:equivalentPropertyowl, owl:propertyDisjointWith}), it is sufficient to remove the last line that ends with a comment.

• sub:non-equivalent_property rdfs:range rdf:Property ;
  owl:propertyDisjointWith owl:equivalentProperty .
sub:non-equivalent_property_nor_subPropertyOf rdfs:subPropertyOf sub:non-equivalent_property ;
  owl:propertyDisjointWith rdfs:subPropertyOf .
• SELECT distinct ?p1 ?p2 WHERE #list each non-complying pair of properties { ?p1 a rdf:Property. ?p2 a rdf:Property. #for each pair of property ?p1 and ?p2 FILTER NOT EXISTS{ ?p1 rdfs:subPropertyOf|owl:equivalentProperty|owl:propertyDisjointWith ?p2 } FILTER NOT EXISTS{ ?p1 sub:non-equivalent_property_nor_subPropertyOf ?p2 } #defined in OWL-RL|QL }

Adaptation of Query 3 for the “every object to some other object” cardinalities.

Adding or lifting restrictions. Queries for CN can be made more restrictive by adding more tests but, as illustrated with Query 2, more tests relax queries for CN–. E.g, more relations or more precise ones may be checked, and the function isIRI() may be used for checking that some classes are named.

Counterparts of the previous queries for the use of CN and C% (instead of CN–, with the same parameters).

3.1.2. Types To State Or Check That Particular Types Are Related By Subtype Or Equivalence Relations, Or Cannot Be So

Shortcuts for combinations of OWL types. This subsection illustrates some of the many type definitions (in the sense given in Section 2.1.3) made in the Sub ontology [Martin, 2019] i) to support the writing of complex specifications, and more importantly, ii) to ease the development of KBs complying with these specifications, especially those leading to types that are “universally complete wrt. generalization, equivalence and exclusion relations”.

Using more complex queries when less powerful inference engines are used. These type definitions are made using OWL but many of them use i) owl:propertyDisjointWith and hence are not in OWL-EL, and ii) owl:unionOf or owl:disjointUnionOf within “a superclass expression” and hence are neither in OWL-RL|QL nor OWL-EL. As illustrated in the previous subsection, even when the inference engine used in conjunction with the SPARQL engine for checking the KB is not powerful enough to fully exploit relations of such types, the results of the checkings are accurate (i.e., complete if CN– is used) if those relations need not be inferred, hence on two conditions. First, the query must check the presence of such relations. Second, when the used inference engine cannot exploit type definitions that include such relations, either the KB always uses such relations instead of the combinations of relations in these definitions, or the query must also check these combinations of relations.

Generalization of OWL types for relations from classes. In this article, sub:Type refers to the supertype of all types, e.g. of all instances of rdfs:Class or rdf:Property. Similarly, the relation types sub:subtypeOf, sub:equivalent_type, sub:disjoint_type, sub:unionOfTypes and sub:disjointUnionOfTypes are the respective generalizations (to all types) of rdfs:subClassOf, owl:equivalentClass, owl:disjointWith, owl:unionOf and owl:disjointUnionOf. To that end, Sub first defines sub:unionOfProperties and sub:disjointUnionOfProperties (based on sub:unionOfProperties and owl:propertyDisjointWith). More precisely, Sub first partially defines those types of relation between properties using OWL (i.e., Sub defines their supertypes and signatures) and then, in a separate file, provides “SPARQL definitions” for them i.e. SPARQL update operations which, when run on a KB, replace the use of such relations between properties by combinations of RDF+OWL relations. For these relations between properties, these SPARQL definitions are mosty only for documentation purposes, not for supporting more inferences, since no current OWL engine would exploit them (e.g., because of their use of lists and, for sub:unionOfProperties, the use of class expression as destination of rdfs:domain and rdfs:range relations). However, these relations between properties are still interesting to use in a KB because i) inference engines that are not restricted to OWL may exploit them, ii) as shown below, their use make the representations easier to read and write, and iii) their partial definition in OWL means that no OWL inference is lost (e.g., an OWL engine would interpret the use of sub:unionOfProperties as simply defining subproperties). As shown in the rest of this subsection and in some other subsections of this article, Sub makes some other generalizations of OWL types from classes.

Using (in-)complete sets of (non-)exclusive subtypes. It seems that an efficient way to build a KB where types are “universally complete wrt. generalization, equivalence and exclusion relations” is, when relating each type to one or several direct subtypes of it, to use i) a subtype partition, i.e. a disjoint union of subtypes equivalent to the subtyped type (that is, a complete set of disjoint subtypes), and/or ii) “incomplete sets of disjoint subtypes”, and/or iii) “(in-)complete sets of subtypes that are not disjoint but still non-equivalent (hence different) and not relatable by subtypeOf relations”. The previous use of “and/or” is meant to convey that a type may have several sets of subtypes, and hence each kind of set is selected for its relevance. However, as illustrated within the next paragraph, this method is not sufficient for the above cited goal since it does not represent whether subtypes belonging to different sets are comparable or not (in general, as observed in the assumptions mentioned in Section 3.1, these subtypes are neither comparable nor in exclusion). Reminder (and adaptation from the more general definition of Section 2.1.3): “comparable types” refer to a set of types that are equivalent or in which one type is a subtype or supertype of the others, while “uncomparable types” refers to types that are in exclusion, i.e., that cannot be equivalent and in which none of the types can be subtype or supertype of the others. One way to see the need for these comparability or uncomparability relations, to reach the above cited goal, is to note that without them the use closed-world assumption or the unique name assumption may lead to more inferences.

Properties easing the use of (in-)complete sets of (non-)exclusive subtypes, and non-exclusion relations between types of different sets. Below is the list of properties that are defined in Sub (using OWL and, generally, SPARQL update operations too) to help representing all the relations mentioned in the previous paragraph, in a concise way, hence in a way that i) is not too cumbersome and prone to errors, and ii) makes the representations more readable and understandable by the readers once the properties are known to these readers.

• sub:pC (partition of classes): for the reasons mentioned in the previous paragraph, this type is actually not just an abbreviation of owl:disjointUnionOf; a relation of this type also states that the subclasses in the partition are neither comparable nor in exclusion with the other subclasses of the same source class.
• sub:eC (exclusive subClasses): to state that the types in the destination list are i) exclusive but that the list is not complete, and ii) neither comparable nor in exclusion with the other subclasses of the same source class.
• sub:cC (complete set of subClasses): like sub:cP but without exclusion relation between the classes of the destination list.
• sub:sC (subClass) which states that each of its destinations is a subclass that neither comparable nor in exclusion with the other subclasses of the same source class. Here is an example:

    :Person  sub:pC (:AdultPerson :NonAdultPerson), (:MalePerson :NonMalePerson) ;
                           #assuming that the distinction Male/Female is complete
             sub:sC  :Driver, :Student, :Caucasian, :HispanicPerson, :SpanishPerson .
  

  Here is what this example representation would be using only OWL properties and sub:nuC (an abbreviation of sub:not_uncomparable_class, a property which is defined below using OWL-RL|QL), abbreviating “Person” by “P”, and not even mentioning the classes Student and :Caucasian (nor the relations from or to them):

  :P  owl:disjointUnionOf  (:AdultP :NonAdultP), (:MaleP :NonMaleP).
  :AdultP  sub:nuC :Driver, :HispanicP, :MaleP, :NonMaleP.
  :NonAdultP  sub:nuC :Driver, :HispanicP, :MaleP, :NonMaleP.
  :Driver rdfs:subClassOf :P;  sub:nuC :HispanicP, :SpanishP, :AdultP, :NonAdultP, :MaleP, :NonMaleP.
  :HispanicP rdfs:subClassOf :P; sub:nuC :SpanishP, :AdultP, :NonAdultP, :MaleP, :NonMaleP.
  :SpanishP rdfs:subClassOf :P;  sub:nuC :AdultP, :NonAdultP, :MaleP, :NonMaleP.
  

  Here is what the example representation would be using only OWL properties, not mentioning the sub:nuC relations, and using an indentation of one character as an attempt to help the reader visualise the subtype hierarchy:

    :P  owl:disjointUnionOf  (:AdultPerson :NonAdultPerson), (:MalePerson :NonMalePerson) .
     :Driver rdfs:subClassOf :Person .      :Student rdfs:subClassOf :Person .
     :Caucasian rdfs:subClassOf :Person . 
     :HispanicP rdfs:subClassOf :Person .   :SpanishP rdfs:subClassOf :Person .  
  

  This last example representation is both less precise and still visually less structured than the first previous one. When an ontology has many relations, any kind of visual structure is important to help design it or understand it.

• sub:pP (partition of properties): the counterpart of sub:pC for properties.
• sub:eP (exclusive subProperties): the counterpart of sub:eC for properties.
• sub:cP (complete set of subProperties): the counterpart of sub:cC for properties.
• sub:sP (subProperty): the counterpart of sub:sC for properties.

For an OWL engine, despite the use of SPARQL definitions and for the reasons given in the third paragraph of this subsection (or similar reasons), using these last four properties is only equivalent to the use of rdfs:subClassOf relations – plus owl:propertyDisjointWith relations when sub:pP or sub:eP is used. On the other hand, via the SPARQL definitions of sub:pC, sub:eC, sub:cC and sub:sC, their use leads to their “nearly full” representation in OWL-RL|QL. This “nearly full” is explained in the next paragraph.

Definition of sub:sC. As an illustration for definitions via OWL and via SPARQL in Sub, here are all those necessary to define sub:sC. The following groups are derived from depency relations between the definitions. Here, all the definitions are in OWL-RL|QL except for the use of sub:unionOfProperties in the definition of sub:comparable_class, and this particular use can be replaced by rdfs:subClassOf relations without consequences on the resuts of checks via queries such as Query 1. This is what “nearly full representation in OWL-RL|QL” means in the previous paragraph, and for sub:pC, sub:eC and sub:cC too since their definitions also reuse sub:comparable_class.

• sub:superClassOf owl:inverseOf rdfs:subClassOf . sub:non-equivalent_class rdfs:range rdfs:Class; owl:propertyDisjointWith ow:equivalent_class .
• sub:comparable_class sub:unionOfProperties (owl:equivalentClass rdfs:subClassOf sub:superClassOf) . sub:uncomparable_class rdfs:subPropertyOf sub:non-equivalent_class ; owl:propertyDisjointWith sub:comparable_class . sub:uncomparable-but-not-disjoint_class rdfs:subPropertyOf sub:uncomparable_class ; owl:propertyDisjointWith owl:disjointWith . #"uncomparable" rather than "non-comparable" is used to highlight that the destination is # "known by the inference engine to be not comparable". The use of owl:propertyDisjointWith # may be insufficient for that but a stronger property (defined at the end of this subsection) # can be used instead, if necessary and if the inference engine can exploit it.
• sub:proper-subClassOf rdfs:subPropertyOf rdfs:subClassOf ; # "strict subclassOf" owl:propertyDisjointWith owl:equivalentClass . sub:proper-superClassOf owl:inverseOf sub:proper-subClassOf ; owl:equivalentProperty sub:proper-subClass .
• #the following definition is a partial one, not a full one, since OWL does not support the # definition of "-with-its-siblings" and hence "uncomparable...-with-its-siblings" sub:proper-superClassOf_a-subclass-uncomparable-but-not-disjoint-with-its-siblings rdfs:subPropertyOf sub:proper-superClassOf ; owl:equivalentProperty sub:proper_subClass_, sub:sC_ . #two abbreviations #the "_" is here used to abbreviate "uncomparable-but-not-disjoint-with-its-siblings"
• #Since OWL cannot directly be used for fully defining the previous relation type, here is # a SPARQL update operation which replaces each sub:sC_ relation by an equivalent set of # simpler relations, the types of which can be fully defined in OWL. DELETE { ?class sub:sC_ ?subC1, ?subC2 } INSERT{ ?class sub:proper-superClassOf ?subC1, ?subC2 . ?subC1 sub:uncomparable-but-not-disjoint_class ?subC2 } WHERE { ?class sub:sC_ ?subC1, ?subC2 . #for any two subclasses ?subC1 and ?subC2 FILTER(?subC1 != ?subC2) }
• #sub:sC_ is handy but, since a class may have some exclusive subclasses, sub:sC is # even more interesting since it allows to state that all the subclasses of a class # are "uncomparable but not disjoint" except for those which are # connected by disjointWith relations (and thereby are already known to be non-equivalent) or # connected by subClassOf relations (and thereby are already known to be non-equivalent). #To that end, 3 cases and hence three SPARQL update operations are necessary: #1) the case that implies sub:sC_ (i.e. when ?subC1 is not comparable/exclusive to ?subC2): DELETE { ?class sub:sC ?subC1, ?subC2 } INSERT{ ?class sub:proper-superClassOf ?subC1, ?subC2 } ?subC1 sub:uncomparable-but-not-disjoint_class ?subC2 } WHERE { ?class sub:sC ?subC1, ?subC2 . #for any two subclasses ?subC1 and ?subC2 FILTER(?subC1 != ?subC2) FILTER NOT EXISTS{ ?subC1 rdfs:subClassOf|owl:equivalentClass ?subC2 } FILTER NOT EXISTS{ ?subC1 ^rdfs:subClassOf|owl:disjointWith ?subC2 } } #2) the case where ?subC1 is comparable to ?subC2: DELETE { ?class sub:sC ?subC1, ?subC2 } INSERT{ ?class sub:proper-superClassOf ?subC1, ?subC2 } WHERE { ?class sub:sC ?subC1, ?subC2 . #for any two subclasses ?subC1 and ?subC2 FILTER(?subC1 != ?subC2) FILTER EXISTS{ ?subC1 sub:comparable_class ?subC2 } } #3) the case where ?subC1 is exclusive to ?subC2: DELETE { ?class sub:sC ?subC1, ?subC2 } INSERT{ ?class sub:proper-superClassOf ?subC1, ?subC2 . WHERE { ?class sub:sC ?subC1, ?subC2 . #for any two subclasses ?subC1 and ?subC2 FILTER EXISTS{ ?subC1 owl:disjointWith ?subC2 } }

In OWL-Full, the use of owl:propertyDisjointWith in definitions such as the above ones may be refined. Some of the previous definitions use owl:propertyDisjointWith. In OWL-Full, a stronger form of negation is more appropriate: the one that the property sub:propertyNegation expresses. It is defined via the two points below. For the above definitions, the use of sub:propertyNegation not only does not seen to bring any interesting precision. However, from now on, if only for explanatory purposes, it is used instead of owl:propertyDisjointWith and it is assumed that the SPARQL update operation below is used when useful, i.e. when the application needs it and when the used inference engine can exploit the generated statements (i.e., when this engine is at least an OWL-Full one).

• sub:propertySymmetricNegation rdfs:subPropertyOf owl:propertyDisjointWith .
• DELETE { ?rt1 sub:propertySymmetricNegation ?rt2 } INSERT{ [] rdf:type owl:NegativePropertyAssertion; owl:assertionProperty ?rt2; owl:sourceIndividual ?indiv1; owl:targetIndividual ?indiv2 . [] rdf:type owl:NegativePropertyAssertion; owl:assertionProperty ?rt2; owl:sourceIndividual ?indiv2; owl:targetIndividual ?indiv1 . } WHERE { ?rt1 sub:propertySymmetricNegation ?rt2 . ?indiv1 ?rt1 ?indiv2 }

Adaptation of queries in the previous subsection for them to use only one relation type. From any object, checking various relations (of different types) to every/some object is equivalent to checking one relation that generalizes these previous relations. The Sub ontology provides types for such generalizing relations since these types ease the writing of queries. However, these types have to be defined using owl:unionOf or owl:disjointUnionOf within “a superclass expression” and hence are neither in OWL-RL|QL nor OWL-EL. E.g.:

• Using the following query – which checks only one relation – is equivalent to using Query 2 (except that it requires an OWL engine not restricted to OWL-RL|QL nor OWL-EL).
  SELECT distinct ?c1 ?c2 WHERE #list each non-complying pair of classes { ?c1 a rdfs:Class. ?c2 a rdfs:Class. #for each pair of classes ?c1 and ?c2 FILTER NOT EXISTS{ ?c1 sub:class_known_to_be_comparable_or_uncomparable ?c2 }
• Checking that from every object there is a sub:class_known_to_be_SUP-comparable_or_exclusive_or_SUP-uncomparable is similarly equivalent to performing the version of Query 2 for the “every object to some object” cardinalities.
• For the other SPARQL queries proposed in this article, Sub provides types for creating similarly equivalent “one relation based” queries.

These general types may also be useful for constraint-based checks, as illustrated in the next subsection.

3.1.3. Checking Classes Via SHACL

For checking 100% compliances. Like OWL, SHACL (Shapes Constraint Language) [Knublauch & Kontokostas, 2017] is a language – or an ontology for a language – proposed by the W3C. Unlike OWL, SHACL supports constraints on how things should be represented within an RDF KB. SHACL can be decomposed into i) SHACL-core, which cannot reuse SPARQL queries, and ii) SHACL-SPARQL, which can reuse them. CN and C% are not boolean functions and hence a full implementation of their use cannot be obtained via SHACL. However, SHACL can be used to check that a KB is 100% compliant with particular specifications expressed via C%.

SHACL counterpart of Query 2. The “every object to every object” cardinalities cannot be checked via SHACL-core but here is the C% related counterpart of Query 2 (Section 3.1.1) in SHACL-SPARQL.

SHACL counterpart of Query 2 for the “every object to some object” cardinalities. Here, SHACL-core can be used.

• sub:Shape_for_the_SUP-comparability_of_every-class_to_some-class a sh:NodeShape; sh:targetClass rdfs:Class; sh:or (#every class has a SUP-comparable class: [sh:path [sh:alternativePath (rdfs:subClassOf owl:equivalentClass)]; sh:minCount 1] #or has a strongly uncomparable class (a disjoint class): [sh:path [sh:alternativePath (owl:complementOf owl:disjointWith)]; sh:minCount 1] [sh:path [sh:inversePath (owl:members [sh:zeroOrMorePath rdf:rest] rdf:first)]; sh:minCount 1; sh:class owl:AllDisjointClasses] [sh:path [sh:inversePath (owl:disjointUnionOf [sh:zeroOrMorePath rdf:rest] rdf:first)]; sh:minCount 1] #or has a weakly SUP-uncomparable class: [sh:path sub:non-equivalent_class_nor_subClassOf; sh:minCount 1] ).
• #or, more concisely: sub:Shape_for_the_SUP-comparability_of_every-class_to_some-class a sh:NodeShape; sh:targetClass rdfs:Class; sh:property[ sh:path sub:class_known_to_be_SUP-comparable_or_exclusive_or_SUP-uncomparable; sh:minCount 1 ].

Use of alternative languages. Other languages could be similarly used for implementing intrinsic completeness evaluations, e.g. SPIN (SParql Inferencing Notation) [w3c, 2011], a W3C language ontology that enables i) the storage of SPARQL queries in RDF and, ii) via special relations such as spin:rule and spin:constraint, the triggering of such queries when this is relevant. More generally, most transformation languages or systems that exploit knowledge representations could be similarly reused. [Svátek et al., 2016] and [Corby & Faron-Zucker, 2015] present such systems. [Martin, 2018] explored the design of “generic SPARQL queries” for checking constraints expressed in RDF+OWL in the evaluated KB. This generic SPARQL query based approach could be reused for ontology (intrinsic) completeness checking purposes.

4. Ontology and Exploitations of Relation Types Useful For the 3^rd Parameter

4.1. Exploitation of All Relations Satisfying Particular Criteria

So far, in all the presented uses of CN and C%, their 2^nd parameter only included particular named types. With uppermost types such as sub:relation or rdf:Property, one may only state very weak constraints, typically that any pair of objects must be connected by some relation, possibly contextualized or negated. With sub:definition-element one may be a bit more precise with still being generic: typically (with no 3^rd parameter), one may state that any pair of objects must be connected by a relation that is at least known to be “true by definition” or known to be “false by definition”. With more precise types, one may state more precise constraints to enforce the use of particular types.

However, one may also want to check that each particular property associated to a class – via relation signatures or the definitions of this class – is used whenever possible (hence with each instance of this class) but in a relevant way, e.g. using negations or contextualized statements when unconditional affirmative statements would be false. Such checking cannot be specified via a few named types in the 2^nd parameter of CN and C%.

This checking may be enforced using constraints (like those in database systems or those in knowledge acquisition or modelling tools). However, with many constraint languages, e.g. SHACL, this checking would have to be specified class by class, or property by property, since the language would not allow quantifying over classes and properties: “for each class, for each property associated to this class”. As defined in Section 2.2, CN and C% have this same restriction but more generic versions can be defined. For example, in the 2^nd parameter, instead of just relation types, CN and C% could accept functions taking as argument the currently evaluated object and returning a set of relation types to check for this object. Then, a function which, for each class, returns the set of the “properties associated to this class” could be specified and used.

Instead, special variables (or keywords) such as “$each_applicable_relation” (which is mentioned in Figure 1) may be used in the list of relation types for the 2^nd parameter of CN or C%. This variable specifies that “all uncomparable relation types (declared in the KB or the KBs it imports) which can be used (e.g., given their definitions or signatures) should be used whenever possible”. When several comparable relation types may be used, only one should be used. The use should not be inferable from a definition or signature: a specialization or instantiation should be provided. When minimum cardinalities are defined for a relation, they are checked too. Most importantly, the checking is always made, hence as if the “every object to some object” cardinalities were specified, even if the “every object to every object” cardinalities are specified. Indeed, if this last default kind of cardinalities was used here, only pairs of already existing objects would be checked and hence no non-existing relation to a non-existing object would be detected as a problem. Since the cardinalities used in the 3^rd parameter are ignored for this variable, this variable may be added to the list of named types in the 2^nd parameter.

A variant of the previous variable may be used for taking into account only definitions. With this variant, every evaluated object must have all the relations prescribed by the definitions associated with the types of the object. Unlike with this variant, when using sub:definition-element in the 2^nd parameter, with the “every object to some object” cardinalities in the 3^rd parameter, every evaluated object must have at least one sub:definition-element relation and needs only have one such relation.

A variant may also be used for only taking into account all definitions of necessary relations. It should be noted that many relations cannot be defined as necessary, e.g., sub:proper-subClassOf relations cannot be defined as necessary for classes, since the uppermost class cannot have such a relation. However, “==>”, “<==>” and “==>!” may be defined as necessary for any object. Thus, if this is done in a KB, using these relation types in the 2^nd parameter of CN or C% in addition to this variant is not necessary.

Here are SPARQL queries that respectively exploit i) rdfs:domain and rdfs:range relations, which for the purpose of this example are assimilated to relation signatures, and ii) class definitions via OWL restrictions. They exploit these relations to check that “properties associated to this class” are used whenever possible, possibly within a negated or contextualized statement.

The KB evaluation measure closest to C% seems to be the one described in [Duan et al., 2011]. The authors call it “coverage of a class (or type) within a dataset” (the authors use the word “type” but a class is actually referred to). This coverage is with respect to the “properties that belong to the class”. For each class and each of its properties, this coverage is the ratio of i) the number of occurrences of this property from the instances of this class, to ii) the number of properties of this class, and (i.e. also divided by) iii) the number of instances of this class (in the evaluated dataset). Hence, this coverage returns 100% when all instances of a class have all the “properties that belong to the class (or type)” (this is the terminology used in [Duan et al., 2011]).

Thus, this coverage metric is akin to intrinsic completeness measures. Unlike CN or C%, it is restricted to the case described in the previous paragraph and, at least according to the used descriptions and terminology, does not take into account negations, modalities, contexts, relation signatures or relations such as rdfs:domain and rdfs:range. More importantly, C% is a ratio between comparable quantities – the number of evaluated objects satisfying a constraint versus the total number of evaluated objects (1 or more) – while the above cited coverage is not and is about only one class. To compare KBs, [Duan et al., 2011] advocates the use of the “coherence of a class (or type) within a dataset”. It is the sum of a weighted average of the coverages of classes, thus not a ratio between comparable quantities.

In [Zaveri et al., 2016], “coverage” refers to the number of objects and properties that are necessary in the evaluated KB for it to be “appropriate for a particular task”. In [Karanth & Mahesh, 2016], the “coverage” of a class or property is the ratio of i) the number of individuals of this class or using this property (directly or via inferences), to ii) the number of individuals in the KB. This last metric is not a intrinsic completeness measure since, for the given type, “being of that type or using that type” is not a constraint or requirement.

4.2. Object Selection Wrt. Quantifiers and Modalities

Quantifiers for the first selection of objects and relations. The definitions of CN and C% for the “every object to every object” default cardinalities and for the “every object to some object” cardinalities have been given in exSection 2.3. Figure 1 showed these two kinds of cardinalities as options to be selected. Via examples, Section 3.1 shows how the second kind of cardinalities can be implemented in SPARQL and SHACL. Section 5.2 also shows a SPARQL query for this second kind of cardinalities. All the other queries are for the default kind of cardinalities. These two kinds are about object selection: given the 1^st parameter of CN and C%, i.e. the type for the source objects, i) “which instances to check?” and, ii) from these instances, and given the relation types in the 2^nd parameter, “which destination objects to check?”. Other variations may be offered for this selection, e.g. i) a type for the destination objects, and ii) whether the source or destination objects should be named (i.e. be named types or named individuals, as opposed to type expressions or blank nodes). Furthermore, one may also want to consider objects which are reachable from the KB. Indeed, a KB may reuse objects defined in other KBs and object identifiers may be URIs which refer to KBs where more definitions on these objects can be found. This is abbreviated by saying that these other KBs or definitions are reachable from the original KB. Similarly, from this other KB, yet other KBs can be reached. However, this notion cannot be implemented with the current features of SPARQL. Nevertheless, below its “Class of the source objects” selector, Figure 1 shows some options based on this last notion and object naming.

Quantifiers for the second selection. Whichever the cardinalities or variation used for this first selection, each relation to check from or between the selected objects also has a source and a destination. Thus, a second selection may be performed on their quantification: the user may choose to accept any quantification (this is the default option) or particular quantifiers for the source or the destination. In Figure 1, “*” is used for referring to any object quantification and thus “* -> *” does not impose any restriction on the quantification of the source and destination of the relations to be evaluated. The rest of this subsection progressively explains the specializations of “* -> *” proposed in Figure 1. Unquantified objects – i.e. named types, named statements and named individuals – are also considered to be universally and existentially quantified. Since type definitions of the form “any (instance of) <Type> is a ...” (e.g., “any Cat is a Mammal” or “Cat rdfs:subClassOf Mammal”) are particular kinds of universal statements, in Figure 1  i) the expression “∀ -> ∃” also covers definitions and ii) three specializations are proposed for the “∀” quantifier.

• “Any” is the quantifier of the head object of definitions of/via necessary conditions, e.g., with “pm” and “TexAvery” being the respective authors of the following definitions (and hence of the defined terms): “any pm:Triangle is (necessarily) a Polygon that has for part ...” and “(any of the) TexAvery:TomTheCat necessarily has white paws”.
• “Every” is the quantifier of the head object of universal statements that are not definitions, and hence that are universally quantified beliefs (as above defined), e.g. “before 2010, every bird seen by TexAvery:TomTheCat had two wings (at least according to TexAvery:TomTheCat)”. Beliefs may be false, unlike definitions which are “true by definition” (even though two definitions may be inconsistent and although some definitions may be strange, e.g. the definition “any pm:Table necessarily flies” which defines a flying thing). This distinction is exploited by the shared-KB edition protocol of WebKB-2 [Martin, 2011]. Alone, OWL allows the representation of definitions with necessary conditions but does not allow the representation of universally quantified beliefs. However, such beliefs can still be represented in various ad-hoc but still OWL-compatible ways. E.g., one way is to type OWL restrictions – or use ad-hoc relations within them if the used inference engine allows it – to specify the author of the statement and to specify that it should be considered as a belief instead of a true definition. This way can be used when i) both kinds of statements should still be exploitable via OWL inference engines, and ii) the difference between them is exploited via complementary means, e.g. SPARQL queries.
• “AnyByDefault” is the quantifier of the head object of definitions of default characteristics (e.g. instead of necessary conditions or characteristics), e.g. “anyByDefault Healthy Carinate_bird can fly”, i.e. until this is inconsistent with another statement, the inference engine may assume that this statement is true. Alone, OWL does not allow the representation of such definitions. However, they can be represented in various ad-hoc but still OWL-compatible ways. E.g., as for the previous point, one way is to type OWL restrictions or use ad-hoc relations within them.

In Figure 1, in addition to “* -> *”, more specialized options are proposed and “∀:every/any/anyByDefault → *” is selected. This option means that when the source of relations are universally quantified, only the three listed kinds of universal quantifications should be used and hence the distinction should be made between beliefs, definitions via necessary conditions and definitions via default characteristics. The option “* → 1..* complete{...}” is also proposed. This option means that the set of destination objects for each selected relation should be represented as either complete or not complete. Here, “complete” means that either the destination objects are known or that at least one type for all of them has been specified, e.g. using owl:allValuesFrom or owl:disjointUnionOf. Stating that a set of destination objects is complete does not take more time – or much more time – than not doing so, but supports more inferences. This has already been argued for and illustrated regarding the use of owl:disjointUnionOf or properties such as sub:sC_ (alias sub:proper-superClassOf_a-subclass-uncomparable-but-not-disjoint-with-its-siblings, defined in Section 3.1.2) when they can be used instead of properties such as owl:unionOf or rdfs:subClassOf.

Representation of some meanings of alethic modalities in languages that do not fully support such modalities. When a set of statements fully satisfies a specification made via C%, none of these statements has an unknown truth value: if they are neither unconditionally false nor unconditionally true, their truth values or conditions for being true are still specified, e.g. via modalities (of truth/beliefs/knowledge/...), contexts or fuzzy logic. In linguistics or logics, alethic modalities indicate modalities of truth, in particular the modalities of logical necessity, possibility or impossibility. There are first-order logics compatible ways – and ad-hoc but OWL-compatible ways – of expressing some of the semantics of these modalities.

• Using beliefs and definitions via necessary conditions, as above defined, are first-order logics compatible ways of expressing some of the semantics of the modalities “not necessarily but possibly true” and “necessarily true”. With this distinction, some important inferences can be drawn, although not all the inferences that the use of an alethic modal logic would support. Furthermore, additional methods must be used to make the distinction between “essential properties” and “contingent properties”, a distinction that is for example an important one in the OntoClean methodology [Guarino & Welty, 2009].
• Using “==>!” relations, i.e. exclusion (alias disjointWith) relations, or definitions that include some negated relations, are ways to express some of the semantics of the “necessarily false” modality. Using beliefs that include some negated relations allow one to express some of the semantics of the “possibly false” modality, along with more precision: who considers the negated relations as false.
• Negating “==>!” relations or using definitions of default characteristics are ways of stating that something is possible. Using meta-statements in a belief (resp. a definition) is one way of specifying spatial/temporal/... conditions for some relations to be possibly true (resp. necessarily true).

Given the particular nature of these different kinds of statements, selecting which kinds should be checked when evaluating a set of objects may be useful.

4.3. Minimal Differentia Between Particular Objects

To improve the understandability of types, as well as enabling more inferences, when defining a type, a best practice (BP) is to specify its similarities and differences with i) each of its direct supertypes (e.g., as in the genus & differentia design pattern), and ii) each of its siblings for these supertypes. [Bachimont, Isaac & Troncy, 2002] advocates this BP and names it the “Differential Semantics” methodology but does not define what a minimal differentia should be, nor generalize this BP to all generalization relations, hence to all objects (types, individuals, statements).

For the automatic checking of the compliance of objects to this generalized BP, i) Figure 1 proposes the option “minimal differentia”, and ii) the expression "minimal differentia between two objects" is defined as referring to a difference of at least one (inferred or not) relation in the definitions of the compared objects: one more relation, one less or one with a type or destination that is semantically different. Furthermore, to check that an object is different from each of its generalizations, a generalization relation between two objects does not count as a “differing relation”.

More precisely, with the option “minimal differentia”, each pair of objects which satisfies all the given requirements – e.g., with the “every object to some object” cardinalities, each pair of objects connected by at least one of the relation types in the 2^nd parameter – should have the above defined “minimal differentia” too. Thus, if sub:partOf is in the 2^nd parameter, pairs of objects in sub:partOf hierarchies are evaluated too. The same pair of objects may then be tested multiple times if the used checking method is not optimized. Alternatively, a more restrictive option, e.g. one that only applies to objects in subtype hierarchies, may also be proposed. Options may also be proposed to allow more precise specifications on the differentia: “at least two differentia relations”, “types for the differentia relations”, etc.

Hence, using CN or C% with the above cited definition is a way to generalize, formalize and check the compliance with the “Differential Semantics” methodology. Section 4.1 highlights that a KB where hierarchies of objects can be used as decision trees is interesting and that one way to achieve this is to use at least one set of exclusive direct specializations when specializing an object. Systematic differentia between objects is an added advantage for the exploitation of such decision trees, for various purposes: knowledge categorization, alignment, integration, search, etc.

Minimal differentia example. If the type Car is subtyped only by Hatchback_car and Sedan_car, satisfying the notion of “minimal differentia” for subtype relations simply means i) (fully) defining Hatchback_car as a Car having for part a hatch, and ii) (partially) defining a Sedan_car as a Car not having for part a hatch. These definitions distinguish the three classes with respect to the “having a hatch” criteria.

SPARQL query. Here is an adaptation of Query 1 from Section 3.1 to check the compliance of classes with the above defined “minimal differentia” option. This adaptation is the addition of one FILTER block (or here two, for efficiency reasons).

4.4. Constraints on Each Shared Genus Between Particular Objects

Besides highlighting some interests of using at least one set of exclusive direct specializations whenever specializing an object, Section 4.2 reminds that this is an easy way to satisfy C%(owl:Thing, {==>, <==>, ==>!}) but notes that the reverse is not true: checking that a KB complies with this specification does not imply the above cited use and resulting KB structure. However, this can be guaranteed via the option “shared genus+exclusionSet” which is listed in Figure 1. Like “minimal differentia”, this option applies to each pair of objects that already satisfies the other requirements. This option means that each pair of these objects O1 and O2 must satisfy the following two constraints.

• O1 and O2 have at least one shared generalization O: “∃O O1==>O ∧ O2==>O”. This constraint is a generalization of a classic best practice for subtype hierarchies: each type hierarchy should have only one uppermost type, typically, owl:Thing.
• O1 and O2 belong to a same set S of exclusive objects: “∃S O1∈S ∧ O2∈S ∧ ∀x∈S,y∈S (x!=y) ===> (x ==>! y)”. This entails that “all the direct specializations of every object in the evaluated portion of the KB are organized into at least one set of exclusive direct specializations”.

Figure 1 proposes a weaker and hence more general option: one with which only the first constraint is checked, not the second. It also proposes other specializations for this weaker option: “ "==>" tree structure ” and “ "==>" join-semilattice structure ”. In the first case, all the specializations of an object are in the same exclusion set. In the second case, any two objects have a least upper bound. Both structures have advantages for object matching and categorization. Other cases, hence other structures, could be similarly specified, typically one for the full lattice structure. This one is often used by automatic categorization methods such as Formal Concept Analysis.

Figure 1 also shows that similar options can be proposed for partOf hierarchies, hence not just for “==>” hierarchies.

4.5. Synthesis of Comparisons With Other Works

5. Ontology and Exploitation of Relation Types Useful For the 2^nd Parameter

5.1. Generic Relations For Generalizations Or Implications, and Their Negations, Hence For Inference Maximization

Overview. This subsection first defines “==>” as a (minimal) supertype of i) “=>”, ii) the type for supertype relations, and iii) the type for generalizations between individuals (objects that are neither types nor statements). This subsection then defines “!==>”, a type for the negation of “==>”, and “==>!”, a type for exclusions between objects. Thus, if C%( {every owl:Thing},{==>,<==>,==>!}) returns 100% for a KB, for any two objects, the used inference engine knows whether these objects are related by “==>”, “<==>”, “!==>” or “==>!”. Thus, in some senses, the number of inferences based on entered or derived relations of such types is maximal. Advantages for this are listed by Section 4, first when the objects are types and then, in Section 4.4, when the objects are individuals or statements. Then, the present subsection generalize “==>” and “==>!” for increasing the number of inferences that are from several objects to another one. Section 5.1 shows that i) relations of two of these generalizations – sub:definition-element and sub:definition-element_exclusion are particularly interesting to check for the detection or avoidance of inconsistencies and redundancies, and ii) given their definitions, such relations can often be automatically inferred (thus, their do not have to be ented by knowledge providers). All formal definitions are in the Peano-Russel notation.

Definition of “==>”. When connecting statements, i.e. relations or sets of relations, “==>” is identical to “=>”. Unlike “=>”, besides statements, “==>” can also connect types as well as individuals. Two partial and informal definitions of “==>” to connecting types are then: i) “if X==>Y, where X and Y are two types respectively fully defined by the (bodies of) the definitions dX and dY, then dX=>dY”, and conversely, ii) “if dX==>dY, where dX and dY are respectively (bodies of) full definitions of X and Y, then X==>Y”. Assuming that, like types, individuals can also potentially be given full definitions, the previous two partial and informal definitions also apply to individuals. A complete and more formal definition of “==>” (between any two objects) is then:

  ∀X,Y  (X==>Y) <=> ( (X=>Y)  ∨  (∀dX,dY ((X =def dX) ∧ (Y =def dY)) => (dX=>dY))
                              ∨  (∃dX,dY  (X =def dX) ∧ (Y =def dY) ∧ (dX==>dY))  ).

Here are some consequences:

• “==>” generalizes the “subtype of” relation between types (i.e. classes and properties in the RDF and OWL terminologies).
• “==>” also generalizes the “specialization of” relation between individuals. E.g., if in a KB there is an individual identified by Seattle-between-2010-and-2015 that is formally defined as representing “Seattle between 2010 and 2015” wrt. the individual identified by Seattle, then the specialization relation between the two can be inferred: Seattle-between-2010-and-2015 ==> Seatle. Conversely, if the first individual is not fully defined, it can be partially defined by asserting this specialization relation.
• To conclude, “==>” can connect any pair of objects of the same kind: types, individuals and statements. The notion of “object” depends on the used representation language, query language, inference engine and query engine: objects are what these engines can find for the content of the variables in the languages they interpret.

Definition of “<==>”. This type is “==>” in both directions. It generalizes the types owl:equivalentClass, owl:equivalentProperty and owl:sameAs.

Comparability and uncomparability (via “==>”). Two objects x and y are comparable via “==>” if and only if:
(x ==> y) ∨ (x <== y) ∨ (x <==> y).
Otherwise they are uncomparable comparable via “==>”. Unless otherwise mentioned, comparability is via “==>” but there are other kinds of comparability, e.g. via partOf relations. Thus, two types x and y are uncomparable if x is not subtype of y, and y is not subtype of x, and x is not equivalent to y.

Definition of “!”. Applied to a statement, “!” leads to its logical negation. In OWL, for relations between individuals, this means using NegativePropertyAssertion. In higher-order languages, stronger forms of negation may be expressed via modalities representing some meanings of “never” or “not possible”. When applied to a class, “!” refers to its complement (owl:complementOf). When applied to a relation type rt, “!” refers to the type which, if used instead of rt in relations, would negate these relations. The next two paragraphs show derived relation types.

Definition of “!==>”. “!==>” is the negation of “==>”: “∀x,y (x !==> y) <==> !(x ==> y)”.

Definition of “==>!”, alias “==>_exclusion”. “==>!” is the type for exclusion relations (via “==>”): “∀x,y (x ==>! y) <==> (x ==> !y)”. Between types, or between statements in traditional logics, such relations are symmetric: “∀x,y (x ==>! y) <==> (y ==>! x)”. In OWL, owl:complementOf relations are particular owl:disjointWith relations and these ones are particular exclusion relations between types. Using ==>!” between two asserted statements leads to an inconsistent KB. One way to avoid this problem is to use “beliefs”, e.g. by systematically contextualizing such statements with respect to their creator.

Definition of “elementOf-==>”, “elementOf-<==>”, “<==>-element and “==>-element”.

• When converted into conjunctive normal form, the premise of an implication may be decomposed into a conjunction of one or more clauses. This for example allows proofs to be decomposed into branches. “clause-of-=>” is a type of relation from a clause that is part of the premise of an implication, to a statement implied by this implication. A definition for “clause-=>” can be:
    ∀cOfP,S  clause-of-=>(cOfP,S) <=> (∃P,cOfP2!=cOfP (P=>S) ∧ (P <=> (cOfP ∧ cOfP))).
  Conversely, “=>-clause” is a type of relation from a statement S to a clause implied by S (i.e., in the conclusion of an implication from S):
    ∀S,cOfC  =>-clause(S,cOfC) <=> (∃C,cOfC2!=cOfC (S=>C) ∧ (C <=> (cOfC ∧ cOfC2))).
  Similarly, “=>-element” is a type of relation from a statement S to a non-statement object (i.e. a type or an individual) used in a clause implied by S:
    ∀S,y  =>-element(S,e) <=> (∃cOfC =>-clause(S,cOfC) ∧ sub:statement_member(e,cOfC).
  sub:statement_member has many language-dependent subtypes. E.g., rdf:subject, rdf:predicate and rdf:object are subtypes of sub:statement_member but can only be used from an RDF reified statement.
• A relation of type sub:NSC-definition_element connects a type or individual X to an object that is sub:statement_member of a definition of X by necessary and sufficient conditions:
    ∀X,y  sub:NSC-definition_element(X,y) <=> (∃dX (X =def dX) ∧ sub:statement_member(dX,y).
  sub:definition-element is a supertype of sub:NSC-definition_element, sub:NC-definition_element and sub:SC-definition_element. In Sub, sub:definition-element_via_OWL is defined with respect to the definitions that can be made via OWL, as illustrated by Box 2 in Section 5.1.1.
• The type sub:<==>-element is the disjoint union of sub:<=>-element and sub:NC-definition_element<=>. The types sub:elementOf-==>, sub:elementOf-<==> and sub:==>-element can be similarly defined.

Definition of “elementOf-==>_exclusion”. “∀X,Y  ==>-element_exclusion(X,Y) <==> (∀e (sub:definition-element(X,e) ==> !(sub:definition-element(Y,e))) ∧ (sub:definition-element(Y,e) ==> !(sub:definition-element(X,e))) )”. As illustrated in Section 5.1, this type is useful in conjunction with “elementOf-==>”.

                         C%(S,{==>!},M)     !==>      C%(S,{==>},M) 
              ⇗               ⇑     ⇑
         C%(S,{==>!,==>},M)          C%(S,{subtypeOrEq},M)     C%(S,{necessaryPartOrEq},M)
          ⇗  ⇖      ⇑         ⇑     ⇑    ⇑ 
C%(S,{==>!,==>,<==>},M)    C%(S,{strictSubtype},M)     C%(S,{Eq},M)  C%(S,{necessaryStrictPart},M)
                    ⇑            ⇑       ⇑ 
                               C%(S,{strictSubtype,Eq,necessaryStrictPart},M)

Legend:
- “S”: any set of objects but the same set for all the above C%
- “M”: any set of additional constraints but the same set for all the above C%
- “⇑”, “⇗”, “⇖”: “==>” relations as previously defined (“!==>” and “==>!” also as previously defined)
- “Eq”: equivalent or identical
- “necessaryPart”: part such that, if the destination ceases to exist, the source too
  (because of this “necessary dependency”, necessaryPart is subtype of “!==>”) 

5.2. Interest of Checking Implication and Generalization Relations

5.2.1. Examples of Inconsistencies Detected Via SubtypeOf Relations and Negations For Them

Section 2.2 gave introductory examples about how the use of subtypeOf relations – or negations for them, e.g. via disjointWith or complementOf relations – supports the detection or prevention of some incorrect uses of all such relations as well as instanceOf relations. The general cause of such incorrect uses is that some knowledge providers do not know the full semantics of some particular types, either because they forgot this semantics or because this semantics was never made explicit. The following two-point list summarizes the analysis of [Martin, 2003] about the most common causes of the 230 exclusion violations that were automatically detected after some exclusion relation were added between some top-level categories of WordNet 1.3 (those which seemed exclusive given their names, the comments associated to them, and those of their specializations). What such violations mean in WordNet is debatable since it is not an ontology but i) in the general case, they can at least be heuristics for bringing more precision and structure when building a KB, ii) most of these possible problems do not occur anymore in the current WordNet (3.1), and iii) the listed kinds of problems can occur in most ontologies.

• Most violations were due to categories specializing both the general category for actions and a category for something which is not an action: most often, an action attribute, an action description or an action result (as for the categories representing some meanings of the words "epilogue" and "interpretation").
• Other causes were the uses of generalization relations between categories instead of other relations, e.g., instead of i) location/place relations (many categories informally defined as battles were classified as both battles and cities/regions), ii) equivalentClass relations (WordNet 1.3 used categories to represent obsolete names), iii) similarTo relations (as between Greek gods and their Roman counterparts), or iv) member relations (in WordNet 1.3, the classification of species was often intertwined with the classification of genus of species).

5.2.2. Reducing Implicit Redundancies Between Types By Systematically Using SubtypeOf or Equivalence Relations (and Negations For Them)

Within or across KBs, hierarchies of types may be at least partially redundant. This expression means that at least some types can be derived from others or could be derived if particular type definitions or transformation rules were added to the KB. Implicitly redundant subtype hierarchies are those with non-automatically detectable redundancies between these hierarchies. One way to reduce such implicit redundancies, and thus later make the hierarchies easier to merge (manually or automatically), is to cross-relate their types by subtypeOf relations or equivalence relations (and, as the next paragraph shows, negations for them), whenever these relations are relevant. Using such relations is also an easy and efficient way of specifying the semantics of these types.

Several research works in knowledge acquisition, model-driven engineering or ontology engineering, e.g. [Marino, Rechenmann & Uvietta, 1990] [Bachimont, Isaac & Troncy, 2002] [Dromey, 2006] [Rector et al., 2012], have advocated the use of tree structures when designing a subtype hierarchy, hence the use of i) single inheritance only, and ii) multiple tree structures, e.g. one per view or viewpoint. They argue that every object of the KB has a unique place in such trees and thus that such trees can be used as decision trees or ways to avoid redundancies (in the same sense as in the previous paragraph), normalize KBs and ease KB handling or searching via queries or navigation. This is true but the same advantages can also be obtained if all the direct subtypes of each type are organized into at least one “set of disjoint direct subtypes”, and preferably a complete one, hence a “subtype partition”. Indeed, to keep these advantages, it is sufficient (and necessary) that whenever two types are disjoint, this disjointness is specified. With tree structures, there are no explicit disjointWith relations but the disjointness is still (implicitly) specified. Compared to the use of multiple tree structures, the use of disjoint subtypes and multiple inheritance has advantages First, this use does not require a special inference engine to handle “tree structures with bridges between them” (e.g. those of [Marino, Rechenmann & Uvietta, 1990] [Djakhdjakha, Hemam & Boufaïda, 2014], instead of a classic ontology. Second, this use requires less work from knowledge providers than creating and managing many tree structures with bridges between them. Furthermore, when subtype partitions can be used, the completeness of these sets supports additional inferences for checking or reasoning purposes. The various above rationales do not imply that views or tree structures are not interesting to use, they only imply that sets of disjoint (direct) subtypes are good alternatives when they can be used instead.

The fact that a KB fully satisfies C%(sub:Type, {==>, <==>, ==>!}) unfortunately does not imply that have all the direct subtypes of each of its types are organized into at least one “set of disjoint direct subtypes“. However, the reverse implication is true: satisfying this second requirement, as shown in Section 3.1.2, is an easy way to satisfy the first – and (in-)complete sets of (non-)disjoint subtypes can be similarly represented. Furthermore, as shown in Section 2.4.5, the 3^rd parameter of C% can be used for setting constraints on each shared generalization (or genus) of two objects and hence for ensuring this second requirement or other structures for the subtype hierarchy: a tree structure, a lattice, etc. As shown in Section 2.4.5, constraints on the minimal differentia between any two objects can also be set for, here too, ensuring the presence of important information for object categorization and object search by queries or navigation.

Methods or patterns to fix (particular kinds of) detected inconsistencies are not within the scope of this article. Such methods are for example studied in the domains of belief/KB revision/contraction/debugging. [Corman, Aussenac-Gilles & Vieu, 2015] proposes an adaptation of KB revision/debugging for OWL-like KBs. [Djedidi & Aufaure, 2009] proposes ontology design patterns for systematically resolving some particular kinds of inconsistencies, especially the violation of exclusion relations.

5.2.3. Increasing Knowledge Querying Possibilities

Alone, subtypeOf or equivalence relations only support the search for specializations (or generalizations) of a query statement, i.e. the search for objects comparable to the query parameter (as defined in Section 2.1.3). The search for objects “not uncomparable via specialization” to the query parameter – i.e. objects for which nothing in the KB states that they are not or cannot be specializations or generalizations of this parameter – is a more general kind of search which is sometimes useful. E.g.:

• Assume that a KB user is searching for lodging descriptions in a KB where sports halls are not categorized as lodgings but are not exclusive with them either, given that they can be used as lodgings when natural disasters occur. Then, querying this KB for (specializations of) “lodgings” does not retrieve sports halls. On the other hand, querying for objects not uncomparable to “lodgings” returns sports halls. Furthermore, if lodgings have been defined as covered areas, such a query does not return uncovered areas such as open stadiums.
• More generally, when a person does not know which exact type to use in a query or does not know what kind of query to use – e.g. a query for the specializations or for the generalizations of the query parameter – a query for objects “not uncomparable” to the query parameter may well collect all and only the objects the person is interested in, if in the KB all or most types are either comparable or uncomparable.
• As another example, querying a KB about “hotels having a bedroom for less than 100$ per night” does not retrieve bedrooms for which the price has not been registered and hence that may be less than 100$ per night. On the other hand, a query for objects “not uncomparable” to “a bedroom for less than 100$ per night” also retrieves bedrooms with unregistered prices.

The more systematically the types of a KB are made either comparable or uncomparable via subtype relations, the more the statements of the KB will be retrievable via comparability or uncomparability based queries.

5.2.4. Exploitation of Implication and Exclusion Relations Between Non-Type Objects

The previous subsection explored completeness checking for “==>” or “==>!” relations between types or via type definitions. This subsection draws parallels for non-type objects: statements (relations, triples, graphs, ...) and individuals. Generalization or implication relations between non-type objects are exploited by many graph-based inference engines, e.g. the one of the knowledge server WebKB-2 [Martin, 2011]. Since RDF+OWL does not provide – nor permit to define – types for these relations, i) the Sub ontology declares terms for them but does not define them, and ii) RDF+OWL inference engine cannot infer such relations. Assuming that “==>”, “<==>” and “==>!” relations have been generated or manually set between non-type objects, they can be checked via SPARQL: once again, the queries of Section 3.1.1 can be adapted. However, expressing relations between statements in RDF+OWL is often not easy – as with reified statements – or involve RDF extensions such as RDF-star [w3c, 2021]. Hence, searching such relations via SPARQL is often not easy either.

As noted in Section 5.1 where “==>” is defined, statements can be connected by generalization or implication relations (as for the statements “John's car is dark red” and “some cars are red”) and individuals too (as for the individuals “Seattle-between-2010-and-2015” and “Seattle”). (An example specification for checking “=>” between statements has also been given in Section 2.3.) Whenever there exists a “==>” relation between statements describing individuals, there is a “==>” relation between these individuals. Similarly, non-types objects can be connected by “<==>” and “==>!” relations. These relations can be manually set or inferred. For individuals, these relations can be inferred if the individuals have definitions and if all the objects in these definitions can be compared via “==>” relations. Between two existential conjunctive statements, a generalization relation is equivalent to a logical implication [Chein & Mugnier, 2008].

Inferring or manually relating non-type objects by “==>”, “<==>” or “==>!” relations has the same advantages as between types but these advantages are less well-known, probably because of the next two reasons. First, between statements, such relations can often be automatically inferred; hence, they are not talked about except for performance issues or completeness issues. Second, relations between individuals are rarely “==>” relations and almost all individuals can be automatically related by “==>!” relations. However, as illustrated by the next three paragraphs, there are several exception cases to these two points.

One case is when individuals are used when types could or should (ontologically) rather be used, as when types of molecules are represented via individuals in chemistry ontologies.

A second case is when a “==>” hierarchy on parts of the definitions of the individuals is automatically generated for indexation purposes, i.e. for knowledge retrieval performance purposes, e.g. via a method akin to Formal Concept Analysis. This hierarchy of generated individuals is generally large and very well organized.

A third case is when (subtypes of) “==>”, “<==>” or “==>!” are used for representing logical argumentation relations (plus physical consequence relations if the definitions provided in Section 2.4.2 are extended to that end). A sub-case is when the edition of a multi-user shared KB is controlled by a KB edition protocol which requires particular argumentation-related “==>”, “<==>” or “==>!” relations. This is the case with the WebKB-2 protocol [Martin, 2011]. It requires a particular intrinsic completeness of the KB statements (or, more exactly, “beliefs”) with respect to relations of the following types: “==>”, “==>”, “corrective_<==”, “non-corrective_<==”, “corrective_==>!”, “non-corrective_==>!”, “corrective_reformulation”, “corrective_alternative” and “statement_instantiation”. The above cited “particular intrinsic completeness” is not a full one in the sense that it does not fully use the “every object to every object” cardinalities but is an approximation of it that is equivalent for the handling of redundancies and conflicts between beliefs. Indeed, whenever an addition to the KB leads the used inference engine to detect a potential redundancy or conflict, the protocol asks the author of the addition to also add relations of the above listed types to resolve the detected problems by making things explicit. Thus, statements are connected whenever this solves a detected potential problem. This protocol ensures that the shared KB remains organized and free of detected redundancies or conflicts, without having to restrict what the users can enter nor forcing them to agree on terminology or beliefs.

5.3. Exploitation of “Definition Element” Relations and Their Exclusions

This subsection 5.1 generalizes Section 4 to any relation that i) connects types (hence not solely subtype or equivalence relations and their negations) or ii) that is involved in a formal object definition, e.g. a part relation used in a class definition.

As introduced in Section 2.4.2, this article considers that the notion of specialization, and hence of definition, can apply to individuals, not just types: the definition of an object is a logic formula that all its instances and all its sub-individuals must satisfy. E.g., an individual representing the city “Seattle” is specialized by its sub-individual representing “Seattle between 2010 and 2015”. A full definition specifies necessary and sufficient conditions that the instances or sub-individuals must satisfy. In OWL, a full definition of a class is made by relating this class to a class expression via an owl:equivalentClass relation. Specifying only necessary conditions – e.g. using rdfs:subClassOf instead of owl:equivalentClass – means making only a partial definition.

5.3.1. Definition of "Definition Element"

An “element of a definition” is a domain object of this definition, i.e. any object (type, individual or statement) which is member of the body of that definition except for objects of the used language (e.g. logical operators even if they are represented via relation types). A “definition element” relation is one that connects the defined object to an element of the definition. E.g., if a Triangle is defined as a “Polygon that has for part 3 Edges and 3 Vertices”, Triangle has for definition elements the types Polygon, Edge, Vertex and part as well as the value 3. The property sub:definition-element – one of the types proposed by the Sub ontology – is the type of all “definition element” relations that can occur. In Sub and Box 2 below, sub:definition-element is given a subtype for each kind of way a definition can be made in OWL. This defines sub:definition-element with respect to OWL definitions. By defining sub:==>-element in an OWL independent way and for any object, Section 2.4.2 provides more general definitions for sub:definition-element or, more precisely, its subtype for definition by necessary conditions (sub:NC-definition_element).

In the previous paragraph, the words “element” and “member of the body of that definition” are also intended to mean that an “element of a definition” is a proper part of a definition: two types related by a sub:equivalent_type relation are not considered definition elements of each other. More precisely, for each type, its sub:definition-element relations are i) its relations to other types except for those relations that are of type sub:equivalent_type, and ii) its (implicit or explicit) relations to access each definition element of its definitions.

A relation may be defined as necessary or non-necessary, e.g. in OWL via the respective use of a “minimum cardinality of 1” or “maximum cardinality of 1” for the destination of the relation. Hence, sub:definition-element can be partitioned into two subtypes: sub:def_necessary-element and sub:def_non-necessary-elem. This first type and sub:equivalent_type relations are the most general specializations of “==>” relations between types. Thus, given the way sub:definition-element_exclusion and sub:def-necessary-elem_exclusion are defined (cf. next paragraph), the following generalization relations are true:

The types sub:definition-element_exclusion and sub:def-necessary-elem_exclusion are the respective counterparts of sub:definition-element and sub:def_necessary-element, like sub:disjoint_type and “==>!” are the respective counterparts of sub:subtypeOf and “==>”. All these counterparts have similar uses. As illustrated below, they can be defined using the sub:propertySymmetricNegation property defined in Section 3.1.2) via SPARQL (the FL version of Sub uses an even stronger or more precise form of negation). Thus, a relation of this type is one that connects an object O to another object that cannot be used for defining O. E.g. to normalize definitions and thus increase logical inference, this relation may be used for preventing processes to be defined with respect to attributes or physical entities.

5.3.2. Avoiding All Implicit Redundancies and Reaching Completeness Wrt. All “Defined Relations”

As explained in Section 4.2, ensuring that objects in a KB are either comparable or uncomparable – i.e., in the case of types, by checking them via CN or C% with “{sub:subtypeOf, sub:equivalent_type}” or a more specialized 2^nd parameter – reduces implicit redundancies between subtype hierarchies. As illustrated by the next three examples, the above cited checking is not sufficient for finding every potential implicit redundancy resulting from a lack of definition, hence for finding every specialization hierarchy that could be derived from another one in the KB if additional particular definitions were given. However, this new goal can be achieved by using “{sub:definition-element, <==>, sub:definition-element_exclusion})” or a more specialized 2^nd parameter. Indeed, this specification implies that for every pair of objects in the KB, one of these objects is defined using the other or none can be defined using the other. This specification also expresses “intrinsic completeness with respect to all defined relations, hence all relations which are true by definition”.

Example 1 (of potential implicit redundancies). It is often tempting to specialize particular types according to particular types of attributes without explicitly declaring these types of attributes and organizing them by specialization relations. E.g., at first thought, it may sound reasonable to declare a type Fair-process without relating it to an attribute type Fairness (or Fair) via a definition such as “any Fair-process has for attribute a Fairness”. However, Fair-process may then be specialized by types such as Fair-process-for-utilitarianism, Fair-process-for-prioritarianism, Fair-process-wrt-Pareto-efficiency, Fair-distribution, Fair-distribution-wrt-utilitarianism, etc. It soon becomes clear that this approach leads to an impractical combinatorial explosion of types since i) every process type can be specialized wrt. a particular attribute type or any combination of particular attribute types, and ii) similar specializations can also be made for attribute types (starting from Fairness) as well as for function types (e.g. starting from Fair-function). Even if the KB is not a large KB shared by many persons, many beginnings of such parallel categorizations may happen, without them being related via definitions. Indeed, the above example with process types and attribute relations to attributes types can be replicated with any type and any relation type, e.g. with process types and agent/object/instrument/time relation types or with physical entity types and mass/color/age/place relation types.

Example 2. Assume a KB where i) a class A is defined wrt. a class B, ii) A has a subclass A' that only differs from A by the fact that its instances are defined to have one more attribute C, e.g. the color blue, and iii) B has a subclass B' that only differs from B by the fact that its instances are defined to have the attribute C. Then, there is a potential redundancy between subtype hierarchies in this KB since A' could be generated from B' instead of being manually declared.

Example 3. This one may seem like a variant of Example 2 but is rather an instantiation of it. Imagine a KB where i) s1 and s2 are XML namespaces referring to two different knowledge sources (e.g. two documents or persons), ii) the class s1:Color is subtyped by the class s1:Red_color, and iii) the class s1:Car has two subtypes, s1:Colored_car (class A in the previous example) and s2:Red_car, independently created by s1 and s2, and respectively defined wrt. s1:Color and s1:Red_color. Then, there is a potential redundancy between some subtype hierarchies in this KB since s2:Red_car could be generated from s1:Colored_car. This could be detected via a SPARQL query exploiting sub:definition-element relations inferred from the definitions. This particular redundancy could also be detected by setting a sub:definition-element_exclusion relation between s1:Car (or its supertype sub:Physical_entity) and s1:Red_color (or its supertype sub:Attribute).

Ensuring that objects are either comparable or uncomparable via “definition element” relations is a way to prevent such (beginnings of) implicit redundant subtype hierarchies: all of them or, if some assumptions are made to save some knowledge entering efforts (as discussed in the next subsection), most or many of them.

SPARQL query for this checking, on classes. Here is a query derived from Query 1 (Section 3.1.1) to implement CN–({every rdfs:Class}, {sub:definition-element, owl:equivalentClass, sub:definition-element_exclusion}), hence with the “every object to every object” default cardinalities. The new parts are in bold characters.

5.3.3. Finding and Avoiding Most Implicit Redundancies

Avoiding all potential implicit redundancies, i.e. making every object comparable or uncomparable to every object in the KB via definitions or “definition-element exclusion” relations, may be a lot of work since “definition-element exclusion” relations can seldom be used between top-level classes. However, the more of such relations and definitions there are, the more the implicit redundancies may be prevented or detected. For some goals, some KB evaluators may assume that enough useful inferences can be made (e.g. for knowledge retrieval and the detection of redundancies or inconsistencies) if each type has a definition.

Then, SPARQL queries can be used for finding some or most potential implicit redundancies. Here is a query that exploits the typical case described by the previous paragraph titled “Example 2”. With the KB of Example 3, “?subC1, ?r1, ?c2” refers to “x:Colored_car, sub:attribute, x:color” and “?subC2, ?r2, ?c2” refers to “y:Red_car, sub:attribute, x:color”.

5.4. Exploitation of Some Other Transitive Relations and Their Exclusions

Like “==>” relations, other transitive relations have similar advantages, although generally to a lesser extent since, except for total order relations, less inferences – and hence less error detections – can generally be performed.

PartOf relations are partial-order relations which are often exploited, e.g. to represent and reason about spatial parts, temporal parts, sub-processes or subsets. In the same way “subtype exclusion” relations can be defined as connecting types that cannot share subtypes or instances, “part exclusion” relations can be defined as connecting individuals that cannot share parts. In OWL:

Figure 3 shows how setting “part” and “part exclusion” relations support the detection of inconsistencies.

  x:Skin  ←part_exclusion→  x:Hair      
      ↖                      ↗     //sub:partOf relations between instances of the connected classes
  x:Dermis                  / 
          ↖                /       //inconsistency detected; the left c_partOf relation should 
            y:Hair_follicle        //  instead be a sub:location relation between the instances 

Like the organization of types into (in-)complete sets of (non-)disjoint subtypes, the organization of individuals into (in-)complete sets of (non-)disjoint subparts would be too cumbersome without the use of particular properties. However, for subparts, many of such properties cannot be directly defined in OWL and then the use of SPARQL update operations is required. Here are some examples.

To ensure that part relations (or their negations) are used in a particular KB whenever this is possible, one may check this KB with C%({every owl:Thing}, {==>, <==>, ==>!, sub:part, sub:part_exclusion}). Here is a SPARQL query (adapted from Query 1 in Section 3.1.1) for checking the individuals of KB with respect to this specification, with the “every object to every object” cardinalities, and using the identifiers sub:implication, sub:equivalence and sub:implication_exclusion for the types “==>”, “<==>” and “==>!”:

Here is the same query but for the “every object to some object” cardinalities. This one can be reused to create a constraint in SHACL Core, as illustrated in Section 3.1.3.

SKOS [w3c, 2019b] is a popular ontology that proposes the relation type skos:broader, and its inverse, skos:narrower. The first one can be seen as a supertype for hierarchical relation types such as rdfs:subClassOf and sub:partOf, although SKOS does not state that skos:broader relations are transitive. To support the checking of intrinsic completeness via such relations, the Sub ontology includes the following definitions:

5.5. Exploitation of Type Relations and Their Exclusions

Using CN({every owl:Thing}, {rdf:type, ...}) – or a version expoiting more relations types – means checking that for any object and any type there is a statement about a type relation from that object to that type. In other words, assuming such a relationship is either true or false – hence, no contextualization, for example – this specification means that, based on the content of the KB, an inference engine should be able to know i) whether any individual of the KB is of any of the declared type, and, similarly, ii) whether any first-order type is of any of the declared second-order types. These declared types may be the results of owl:imports directives. Thus, if types from foundational ontologies (e.g. BFO or DOLCE [Guarino, 2017], and UFO [Guizzardi et al., 2015]) – or second-order types from ontological methodologies (e.g. OntoClean [Guarino & Welty, 2009]) – are imported into the KB, using the above specification means checking that the KB fully uses – and hence complies with – these ontologies and methodologies, e.g. their partitions for particular types or individuals.

If the imported ontologies or KBs are not precise or organized enough, completing them to satisfy the above specification can be cumbersome. This work can be strongly reduced by using variants of CN (and hence of C%) with more parameters, e.g. one for indicating a precise subset for the destinations of the rdf:type relations. Here are three SPARQL queries that check the above specification but with restrictions on the evaluated relations. In these SPARQL implementations, restrictions are hard-coded.

5.6. Synthesis of Comparisons With Other Works

6. Conclusion

Some technical highlights of the approach. The intrinsic ontology completeness notions and, more generally the intrinsic completeness notions, are the product of many sub-notions. This article showed i) some important sub-notions (Figure 1 is a synthesis and the beginning of a categorization), ii) that few functions are needed for specifying and checking this product, and iii) that the proposed approach also enables the automatic checking and generalization of some KB design recommendations and related “KB quality measures”. The provided examples and evaluation showed some useful specifications which are rarely complied with (even by some top-level ontologies) but would be easy to comply with. Current KB evaluation measures that can be categorized as intrinsic completeness measures have far less parameters and do not exploit aboutness. Thus, they do not answer the research questions of this article. The metrics used by many of such measures are not simple ratios between comparable quantities (quantities of same nature): the proposed approach can use these metrics (4^th parameter of C*) or, as illustrated near the end of Section 2.2 (Comparison to the measure named “coverage” in [Duan et al., 2011]), can sometimes provide more intuitive alternatives.

More in-depth technical highlights.

• In addition to options, primitive relations – logical ones and others such as partOf relations – and their advantages, are explored and generalized, as a way of maximizing inference possibilities and the detection or avoidance of redundancies and inconsistencies. To that end, for example, i) the subtypes and “===>” relations are extended by “==>”, “definition element”, “==>-element” and “elementOf-==>” relations, and ii) classic exclusion relations between types are extended to individuals and statements, and similar exclusion relations are designed for partOf relations and definition element relations. As illustrated by Figure 2 and Box 1, such generalizations also support the possibility of categorizing intrinsic completeness criteria or measures into one specialization hierarchy. Section 5.3 and Section 2.4.3 show that, with the proposed approach, the use of type relations (and exclusions for them) and keywords such as “$each_applicable_relation” allow flexible specifications of checks about the use of i) particular vocabularies, top-level ontologies or methodologies, and ii) common criteria or BPs, including those relying on the exploitation of terms from external ontologies. Sections 2.4.4 to 2.4.6 show that, combined with some other parameters, simple options for the 3^rd parameter of CN or C% are also ways of ensuring the systematic use and normalization of the KB with respect to particular representation approaches (e.g. regarding modalities or contextualizations) and structures: trees, lattices, minimal differentia, etc.
• This article shows that CN, CN– and C% can be implemented via SPARQL queries on OWL KBs, for particular simple kinds of cases but common and interesting ones. Alternatively, constraints may also be used, e.g. SHACL ones in simple cases. More generally, as noted, most transformation languages or systems that exploit knowledge representations could be similarly reused. Besides illustrating the advantages of the proposed approach, this article shows that complying with intrinsic completeness BPs is not necessarily difficult, even with seemingly demanding options like the “every object to every named object” cardinalities, and with languages such as OWL when complemented by SPARQL. E.g., the Sub ontology defines relation types allowing the entering of (in-)complete sets of (non-)exclusive subtypes as easily as solely entering subClassOf relations. As illustrated, their use increases both knowledge entering easiness and knowledge clarity, regarding the existence or absence of specialization, equivalence or exclusion relations from an object to other ones. The evaluation performed on DOLCE+DnS Ultralite confirms some advantages of systematically using exclusion relations – hence such sets, if only for classes – or, conversely, some drawbacks of not using them.
• The introduction highlighted the distinction – and exclusion – between extrinsic model based completeness and intrinsic completeness. However, (extrinsic model based) completeness oracles can reuse intrinsic completeness measures for some of their heuristics, and hence can reuse some results from this article.
• The CN and C% functions have however a feature that may be counter-intuitive: adding a type to a KB may decrease the values returned by these functions. To keep this completeness at 100%, some statements may have to be added to take into account the new type. This may be counter-intuitive to people who think that adding an object to a KB should always increase a measure of its completeness, intrinsic or not. Although this peculiarity does not seem a problem when checking only one KB, e.g. for knowledge acquisition purposes, it has to be kept in mind when comparing KBs. One way to cope with it – or actually exploit it – is to compare the KBs on their use of the same set of types.

Next steps.

• Figure 1 organizes some primitive relation types into a specialization hierarchy. Box 1 (Section 3.3.2) shows the beginning of an ontology of criteria and relation types used in KB design recommendations and KB quality measures. A next step is to add and organize non-primitive types into this hierarchy to provide at least one way to implement an intrinsic completeness evaluation for each criteria listed in Box 1. Since different sources (W3C, ...) advocate the use of different but similar relation types for complying with the listed criteria and BPs, these types will be aligned in the above cited hierarchy. This ontology will be completed and exploited by the code and user interface made for implementing and validating the approach described in this article.
• This approach will be exploited to generalize the KB editing protocol of the KB sharing server WebKB-2 [Martin, 2011] and enable its users to adapt it.
• This approach will also be applied for checking relations automatically extracted from structural dependencies within software code (programs, library of software components, etc.), e.g. for checking the universal completeness of various types of partOf and generalization relations between software objects (functions, structures, variables, etc.).

Acknowledgments. Thanks to Olivier Corby for his help or feedback regarding Corese, the SPARQL queries, the SHACL constraints and various sentences of this article.

7. References

1. Bachimont B., Isaac A., Troncy R. (2002). Semantic Commitment for Designing Ontologies: A Proposal. In: EKAW 2002, Knowledge Engineering and Knowledge Management: Ontologies and the Semantic Web, LNCS, volume 2473, pp. 114–121, Springer Berlin, Siguenza, Spain.
2. Bhattacharyya P. & Mutharaju R. (2022). OntoSeer--A Recommendation System to Improve the Quality of Ontologies. arXiv preprint arXiv:2202.02125.
3. Chein M., Mugnier M. (2008). The BG Family: Facts, Rules and Constraints. Graph-based Knowledge Representation - Computational Foundations of Conceptual Graphs. Chapter 11 (pp. 311–334), Springer-Verlag London, 428p.
4. Corby O., Faron-Zucker C. (2015). STTL: A SPARQL-based Transformation Language for RDF. In: WEBIST 2015, 11th International Conference on Web Information Systems and Technologies, Lisbon, Portugal.
5. Corman J., Aussenac-Gilles N., Vieu L. (2015). Prioritized Base Debugging in Description Logics. In: JOWO@IJCAI 2015.
6. Cuenca J., Larrinaga F., Curry E (2020). MODDALS Methodology for Designing Layered Ontology Structures. Applied Ontology, vol. 15(2), pp. 1–33, 27 January 2020.
7. Djakhdjakha L., Mounir H., Boufaïda Z. (2014). Towards a representation for multi-viewpoints ontology alignments. In: IJMSO, International Journal of Metadata, Semantics and Ontologies, 9(2), pp. 91–102, Inderscience Publishers, Geneva.
8. Djedidi R., Aufaure M. (2009). Ontology Change Management. In: I-SEMANTICS 2009, pp. 611–621
9. Dodds L., Davis I. (2012). Linked Data Patterns – A pattern catalogue for modelling, publishing, and consuming Linked Data, http://patterns.dataincubator.org/book/, 56 pages, 2012-05-31.
10. Dromey R.G. (2006). Scaleable Formalization of Imperfect Knowledge. In: AWCVS 2006, first Asian Working Conference on Verified Software, pp. 29–31, Macao SAR, China.
11. Duan S., Kementsietsidis A., Srinivas K., Udrea O. (2011). Apples and Oranges: A Comparison of RDF Benchmarks and Real RDF Datasets. In: ACM SIGMOD (Special Interest Group on Management of Data) 2011, pp. 145-156.
12. Farias Lóscio B., Burle C., Calegari N. (2017). Data on the Web Best Practices. W3C Recommendation 31 January 2017. Web document: https://www.w3.org/TR/dwbp/
13. Gangemi A. (2019). Ontology:DOLCE+DnS Ultralite. Web document: http://ontologydesignpatterns.org/wiki/Ontology:DOLCE+DnS_Ultralite
14. Galárraga L., Hose K., Razniewski S. (2017). Enabling completeness-aware querying in SPARQL. In: WebDB 2017, pp. 19–22, Chicago, IL, USA.
15. Gómez-Pérez A (1996). Towards a framework to verify knowledge sharing technology. Expert Systems with applications 11.4, 519-529.
16. Gruber T. (2016). Ontology. In: Liu L., Özsu M. (eds) Encyclopedia of Database Systems. Springer, New York, NY. https://doi.org/10.1007/978-1-4899-7993-3_1318-2
17. Grüninger, M., & Fox, M. S. (1995). Methodology for the Design and Evaluation of Ontologies. In: IJCAI Workshop on Basic Ontological Issues in Knowledge Sharing, Montreal, Canada.
18. Guarino G., Welty C. (2009). An Overview of OntoClean. Handbook on Ontologies (Springer, DOI: 10.1007/978-3-540-92673-3_9), pp 201-220, May 2009.
19. Guarino G. (2017). BFO and DOLCE: So Far, So Close. Cosmos + Taxis 4 (4):10-18 (2017). See also: http://www.loa.istc.cnr.it/dolce/overview.html
20. Guizzardi G., Wagner G., Almeida J.P.A., Guizzardi R.S.S. (2015). Towards ontological foundations for conceptual modeling: The unified foundational ontology (UFO) story. Applied Ontology (Online), vol. 10, pp. 259-271, 2015. Other articles on UFO and OntoUML are available from https://nemo.inf.ufes.br/publications/peer-reviewed/
21. Hammer C. & Snelting G. (2009). Flow-sensitive, context-sensitive, and object-sensitive information flow control based on program dependence graphs. International Journal of Information Security, volume 8, pages 399–422. https://doi.org/10.1007/s10207-009-0086-1
22. Hartmann J., Spyns P., Giboin A., Maynard D., Cuel R., Suárez-Figueroa M.C., Sure Y. (2005). D1.2.3 Methods for ontology evaluation. EU-IST Network of Excellence (NoE) IST-2004-507482 KWEB Deliverable D1.2.3 (WP 1.2).
23. Hogan A., Blomqvist E., Cochez M., d'Amato C., Melo G.D., Gutierrez C., Kirrane S., Gayo J.E.L., Navigli R., Neumaier S., Ngomo A.C.N. (2021). Knowledge graphs. ACM Computing Surveys (CSUR), 54(4), pp. 1-37.
24. Karanth P., Mahesh K. (2016). Semantic Coverage Measures: Analytic Operators for Ontologists. In: KDIR 2016, 8th International Conference on Knowledge Discovery and Information Retrieval, Porto, Portugal, November 2016.
25. Kehagias D.D., Papadimitriou I., Hois J., Tzovaras D., Bateman J. (2008). A methodological approach for ontology evaluation and refinement. In: ASK-IT Final Conference. June.(Cit. on p.), pp. 1–13.
26. Kejriwal M., Knoblock C.A., Szekely P. (2021). Knowledge graphs: Fundamentals, Techniques, and Applications. MIT Press.
27. Knublauch H., Kontokostas D. (2017). Shapes Constraint Language (SHACL). W3C Recommendation 20 July 2017. Web document: https://www.w3.org/TR/shacl/
28. Kondylakis H., Nikolaos A., Dimitra P., Anastasios K., Emmanouel K., Kyriakos K., Iraklis S., Stylianos K. & Papadakis N. (2021). Delta: A Modular Ontology Evaluation System. Information, 12(8), 301.
29. Marino O., Rechenmann F., Uvietta P. (1990). Multiple Perspectives and Classification Mechanism in Object-Oriented Representation. In: ECAI 1990, pp. 425–430, Pitman Publishing London, Stockholm, Sweden.
30. Martin Ph. (2003). Correction and Extension of WordNet 1.7. In: ICCS 2003 (Springer, LNAI 2746, pp. 160–173), Dresden, Germany, July 21-25, 2003.
31. Martin Ph. (2009). Towards a collaboratively-built knowledge base of&for scalable knowledge sharing and retrieval. HDR thesis (240 pages; “Habilitation to Direct Research”), University of La Réunion, France, December 8, 2009.
32. Martin Ph. (2011). Collaborative knowledge sharing and editing. International Journal on Computer Science and Information Systems (IJCSIS; ISSN: 1646-3692), Volume 6, Issue 1, pp. 14–29, 2011.
33. Martin Ph. (2018). Evaluating Ontology Completeness via SPARQL and Relations-between-classes based Constraints. In: IEEE QUATIC 2018 (pp. 255–263), 11th International Conference on the Quality of Information and Communications Technology, Coimbra, Portugal, September 4-7, 2018.
34. Martin Ph. (2019). The Sub Ontology in Turtle. Web document: http://www.webkb.org/kb/it/o_KR/p_kEvaluation/ontology/sub/
35. Martin Ph. (2020). DOLCE+DnS Ultralite (DUL) in FL. Web document: http://www.webkb.org/kb/it/o_KR/o_KB/o_upperOntology/dolce/d_dul_fl.html
36. McDaniel M., Storey V.C. (2019). Evaluating Domain Ontologies: Clarification, Classification, and Challenges. ACM Computing Surveys (CSUR), 52(4):1-44. https://doi.org/10.1145/3329124
37. Mendes P.N., Bizer C., Miklos Z., Calbimonte J.P., Moraru A., Flouri G. (2012). D2.1 Conceptual model and best practices for high-quality metadata publishing. Delivery 2.1 of PlanetData, FP7 project 257641
38. Ning H., Shihan D. (2006). Structure-Based Ontology Evaluation. In: ICEBE 2006, Shanghai, pp. 132–137, doi: 10.1109/ICEBE.2006.97.
39. Poveda-Villalón M., Gómez-Pérez A., Suárez-Figueroa M. (2014). OOPS! (OntOlogy Pitfall Scanner!): An On-line Tool for Ontology Evaluation. Int. J. Semantic Web Inf. Syst. 10(2), pp. 7–34. See also http://oops.linkeddata.es/catalogue.jsp
40. Presutti V., Gangemi A. (2008). Content Ontology Design Patterns as practical building blocks for web ontologies. In: ER 2008, Spain (2008). See also http://ontologydesignpatterns.org
41. Rector A., Brandt S., Drummond N., Horridge M., Pulestin C., Stevens R. (2012). Engineering use cases for modular development of ontologies in OWL. Applied Ontology, 7(2), pp. 113–132, IOS Press.
42. Raad J., Cruz C. (2015). A survey on ontology evaluation methods. In: IC3K 2015, Lisbon, Portugal, pp. 179–186. https://hal.archives-ouvertes.fr/hal-01274199/document
43. Reiz A., Dibowski H., Sandkuhl K. & Lantow, B. (2020). Ontology Metrics as a Service (OMaaS). In: KEOD 2020, pp. 250-257, SCITEPRESS Digital Library.
44. Rousset MC. (2004). Small Can Be Beautiful in the Semantic Web. In: ISWC 2004, pp. 6-16, LNCS 3298, Springer. https://doi.org/10.1007/978-3-540-30475-3_2
45. Roussey C., Corcho Ó., Vilches Blázquez L.M. (2009). A catalogue of OWL ontology antipatterns. In: K-CAP 2009, Redondo Beach, CA, USA, pp. 205–206.
46. Ruy F.B., Guizzardi G., Falbo R.A., Reginato C.C., Santos V.A. (2017). From reference ontologies to ontology patterns and back. Data & Knowledge Engineering, Volume 109, Issue C, May 2017, pp. 41–69, DOI: https://doi.org/10.1016/j.datak.2017.03.004.
47. Schober D., Tudose I., Svátek V., Boeker M. (2012). OntoCheck: verifying ontology naming conventions and metadata completeness in Protégé 4. Journal of Biomedical Semantics, 3, S4 (2012). https://doi.org/10.1186/2041-1480-3-S2-S4
48. Šváb-Zamazal1 O., Scharffe F., Svátek V. (2009). Preliminary Results of Logical Ontology Pattern Detection Using SPARQL and Lexical Heuristics. In: WOP 2009 (CEUR Workshop Proceedings, vol. 516, pp. 139–146), Washington D.C., USA.
49. Sowa J.F. (2000). Knowledge Representation: Logical, Philosophical, and Computational Foundations. Brooks/Cole Publishing Co., Pacific Grove, CA.
50. Svátek V., Dudá D. Zamazal O. (2016). Adapting ontologies to best-practice artifacts using transformation patterns: Method, implementation and use cases. Journal of Web Semantics, 40: 52–64. October 2016, https://doi.org/10.1016/j.websem.2016.07.002
51. Tambassi T. (2021). Completeness in Information Systems Ontologies. Axiomathes. https://doi.org/10.1007/s10516-021-09598-9
52. Tartir S., Arpinar I.B., Moore M., Sheth A.P. & Aleman-Meza B. (2005). OntoQA: Metric-based ontology quality analysis. In the proceedings of the IEEE Workshop on Knowledge Acquisition from Distributed, Autonomous, Semantically Heterogeneous Data and Knowledge Sources at ICDM 2005, pages 45-53, November 2005.
53. Vrandečić D. (2010). Ontology Evaluation. PhD thesis, Karlsruhe Institute of Technology. http://www.aifb.kit.edu/images/b/b5/OntologyEvaluation.pdf
54. Vrandečić D. & Sure Y. (2007). How to design better ontology metrics. In: ESWC 2007 Conference (pp. 311-325, Springer).
55. w3c (2009a). Named Graphs. Web document: https://www.w3.org/2004/03/trix/
56. w3c (2009b). SKOS Simple Knowledge Organization System - Reference. W3C Recommendation 18 August 2009, Web document: https://www.w3.org/TR/skos-reference/
57. w3c (2011). SPIN - Modeling Vocabulary. W3C Member Submission 22 February 2011, Web document: https://www.w3.org/Submission/spin-modeling/
58. w3c (2012a). OWL 2 Web Ontology Language – Structural Specification and Functional-Style Syntax (Second Edition). W3C Recommendation 11 December 2012, Web document: https://www.w3.org/TR/owl2-syntax/
59. w3c (2012b). OWL 2 Web Ontology Language Profiles (Second Edition). W3C Recommendation 11 December 2012, Web document: http://www.w3.org/TR/owl2-profiles/
60. w3c (2013a). SPARQL 1.1 Query Language. W3C Recommendation 21 March 2013, Web document: https://www.w3.org/TR/sparql11-query/
61. w3c (2013b). SPARQL 1.1 Entailment Regimes. W3C Recommendation 21 March 2013, Web document: http://www.w3.org/TR/sparql11-entailment/
62. w3c (2014a). RDF Schema 1.1. W3C Recommendation 25 February 2014, Web document: https://www.w3.org/TR/rdf-schema/
63. w3c (2014b). RDF 1.1 Turtle Terse RDF Triple Language. W3C Recommendation 25 February 2014, Web document: https://www.w3.org/TR/turtle/
64. w3c (2014c). RDF 1.1 N-Quads. A line-based syntax for RDF datasets. W3C Recommendation 25 February 2014, Web document: https://www.w3.org/TR/n-quads/
65. w3c (2014d). Best Practices for Publishing Linked Data. W3C Working Group Note 09 January 2014, Web document: http://www.w3.org/TR/ld-bp/
66. w3c (2016). Linked Data. Web document: https://www.w3.org/wiki/LinkedData
67. w3c (2017). Shapes Constraint Language (SHACL). W3C Recommendation 20 July 2017, Web document: https://www.w3.org/TR/shacl/
68. w3c (2021). RDF-star and SPARQL-star. Final Community Group Report 17 December 2021. Web document: https://www.w3.org/2021/12/rdf-star.html
69. Welty C. (2010). Context Slices. http://ontologydesignpatterns.org/wiki/Submissions:Context_Slices
70. Wilson, S. I., Goonetillake, J. S., Ginige, A., & Walisadeera, A. I. (2022). Towards a Usable Ontology: The Identification of Quality Characteristics for an Ontology-Driven Decision Support System. IEEE Access, 10, pp. 12889-12912.
71. Zaveri A., Rula A., Maurino A., Pietrobon R., Lehmann J., Auer S. (2016). Quality assessment for linked data: A survey. Semantic Web, 7(1), pp. 63–93.
72. Zhioua Z. (2017). Specification and Automatic Verification of Security Guidelines for Program Certification. PhD thesis, Télécom ParisTech, 8 September 2017.